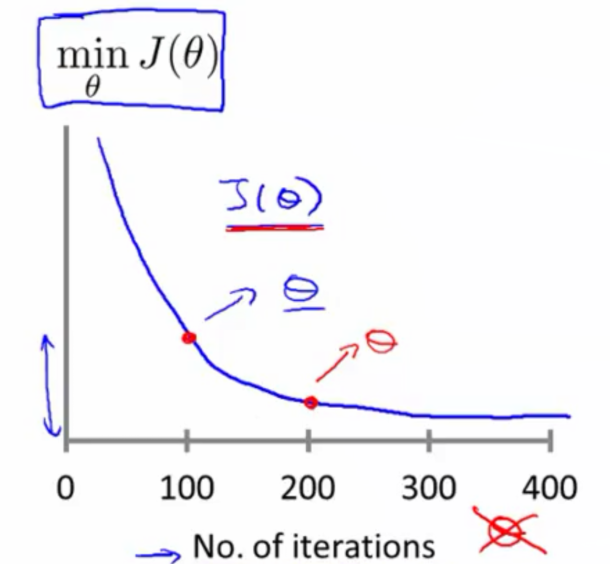
梯度下降法
导数
考虑一元函数$y=f(x)$,它的导数$f’(x)$或$\frac{dy}{dx}$代表了$f(x)$在点$x$处的斜率。对于一个很小的$\epsilon$,我们可以进行近似估计$f(x+\epsilon)=f(x)+\epsilon{f}’(x)$
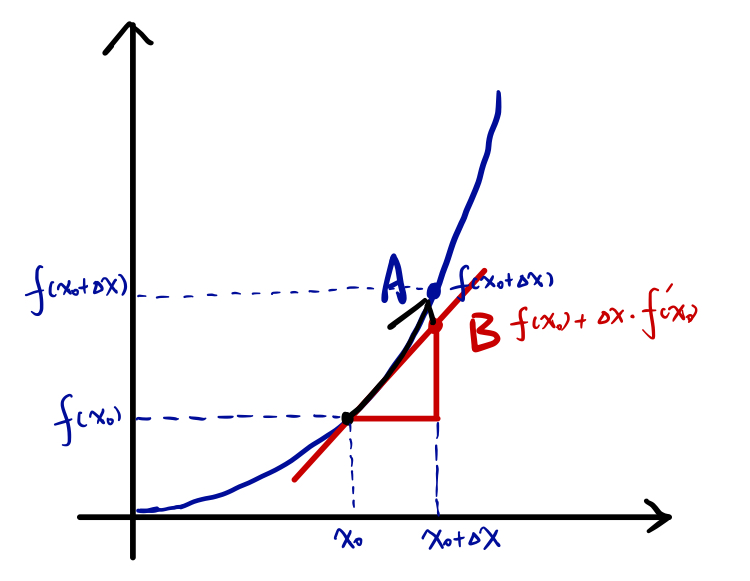
因此导数对于最小化一个函数很有用,他告诉我们如何更改$x$来略微的改善$y$。
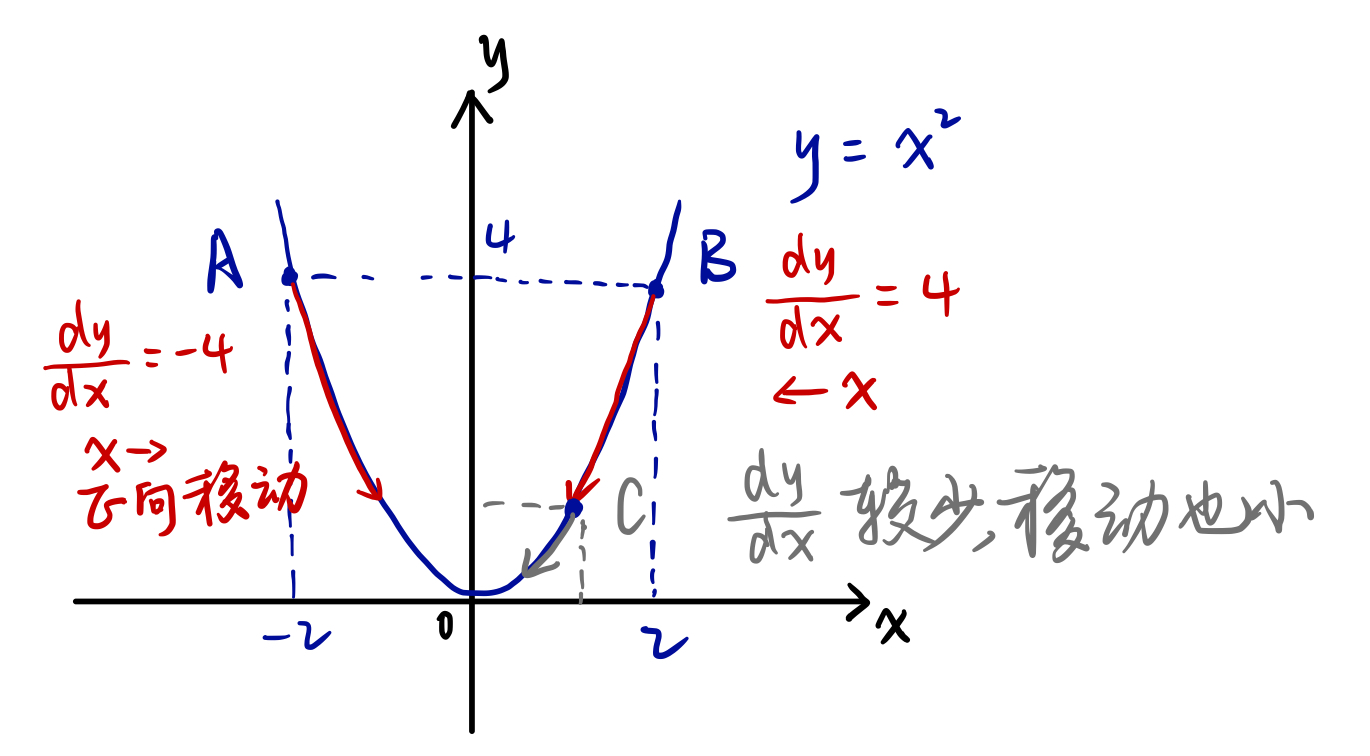
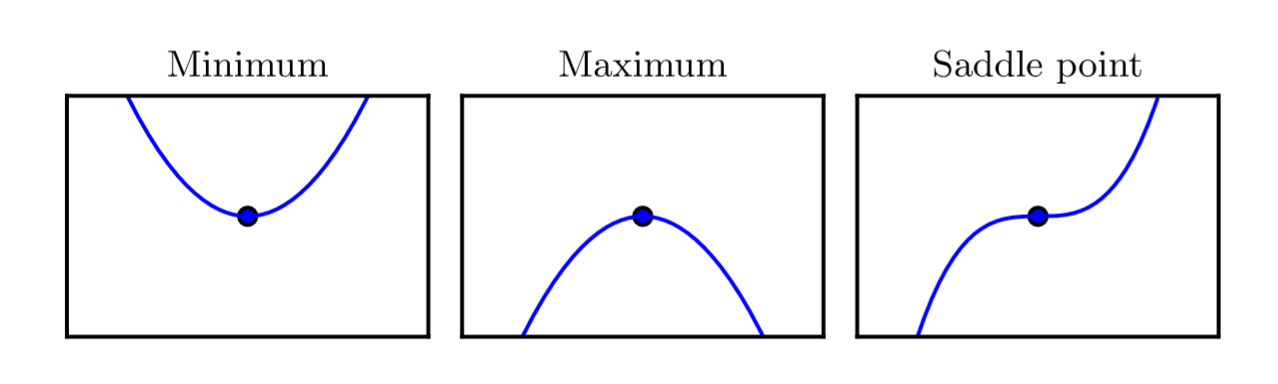
当$f’(x)=0$时,导数无法提供往哪个方向移动的信息。$f’(x)=0$的点称为临界点或驻点。又有三种类型:
极小点(Minimum)、极大点(Maximum)和鞍点(Saddle point)
梯度
对于多维输入的函数,我们需要用到偏导数的概念。
偏导数$\frac{\partial}{\partial{x}_i}f(\boldsymbol{x})$衡量的是,在点$\boldsymbol{x}$处只有$x_i$增加时$f(\boldsymbol{x})$是如何变化的。
梯度是包含所有偏导数的向量,记为$
\nabla_{\boldsymbol{x}}f(\boldsymbol{x})$
多维的情况下,临界点是梯度中所有元素都为零的点。
证明梯度是下降最快的方向:
引入方向导数这一概念。
在$\boldsymbol{\mu}$方向的方向导数是函数$f$在$\boldsymbol{\mu}$方向的斜率,即$f(\boldsymbol{x}+\alpha\boldsymbol{\mu})$关于$\alpha$的导数。
越大的方向导数,表示在这一方向的斜率越大,下降越快。(三维视觉上的体现也越陡)
其中$||\boldsymbol{\mu}||_2=1$,梯度大小不与$\boldsymbol{\mu}$有关,所以等价于$\underset{\boldsymbol{\mu}}{\min}cos\theta$
这在$\boldsymbol{\mu}$和梯度方向相反时取得最小。
梯度下降建议更新的点为:
其中$\epsilon$被称为学习率
全局最小点和局部最小点
使$f(x)$取得绝对的最小值的点是全局最小点,这也是我们最小化问题中,最向往的点。很多时候还存在好多局部极小点或者处于平坦区域的鞍点。
我们通过梯度下降找到的点,一定是一个极小点或者鞍点(不能是极大点,毕竟梯度下降,梯度上升才是找极大点)。
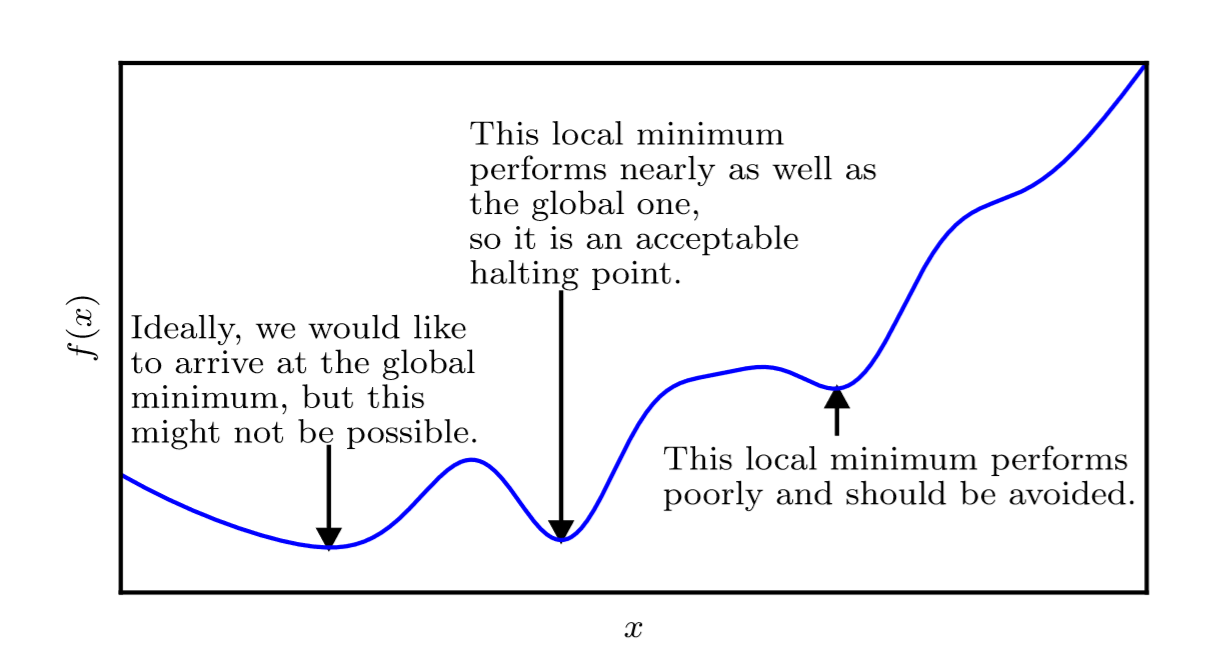
近似最小化。当存在多个局部极小点或平坦区域时,优化算法可能无法找到全局最小点。在深度学习的背景下,即使找到的解不是真正最小的,但只要它们对应于代价函数显著低的值,我们通常就能接受这样的解。
Gradient Descent in Practice I-Feature Scaling(吴恩达ML)
为什么要进行特征缩放?
考虑一个例子。现在有一个二维的线性回归模型
第一种情况,$x1\in[0,2000]$,$x2\in[0,5]$。
此时,我们的损失函数$J(\theta)$的轮廓图可能是一个又瘦又长的椭圆,我们对$J(\theta)$进行梯度下降的时候,可能会走一些弯路。
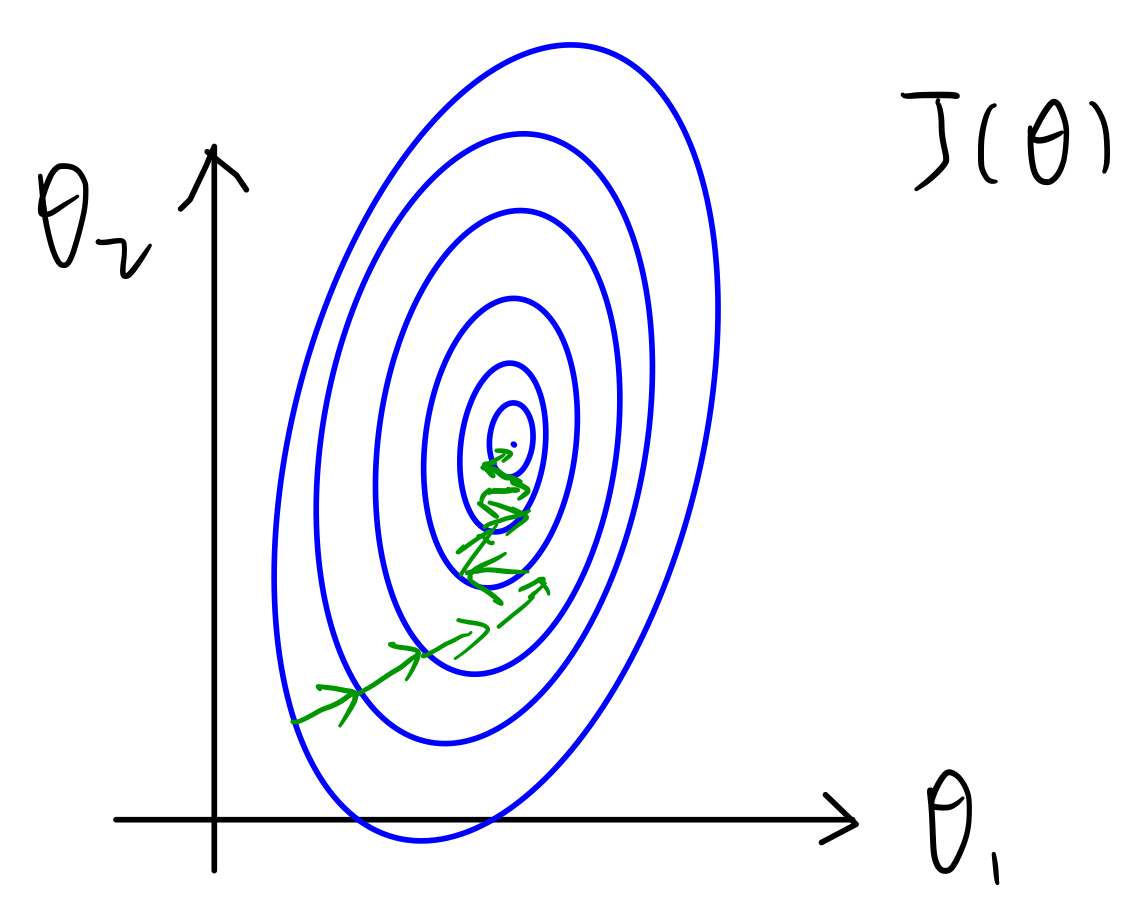
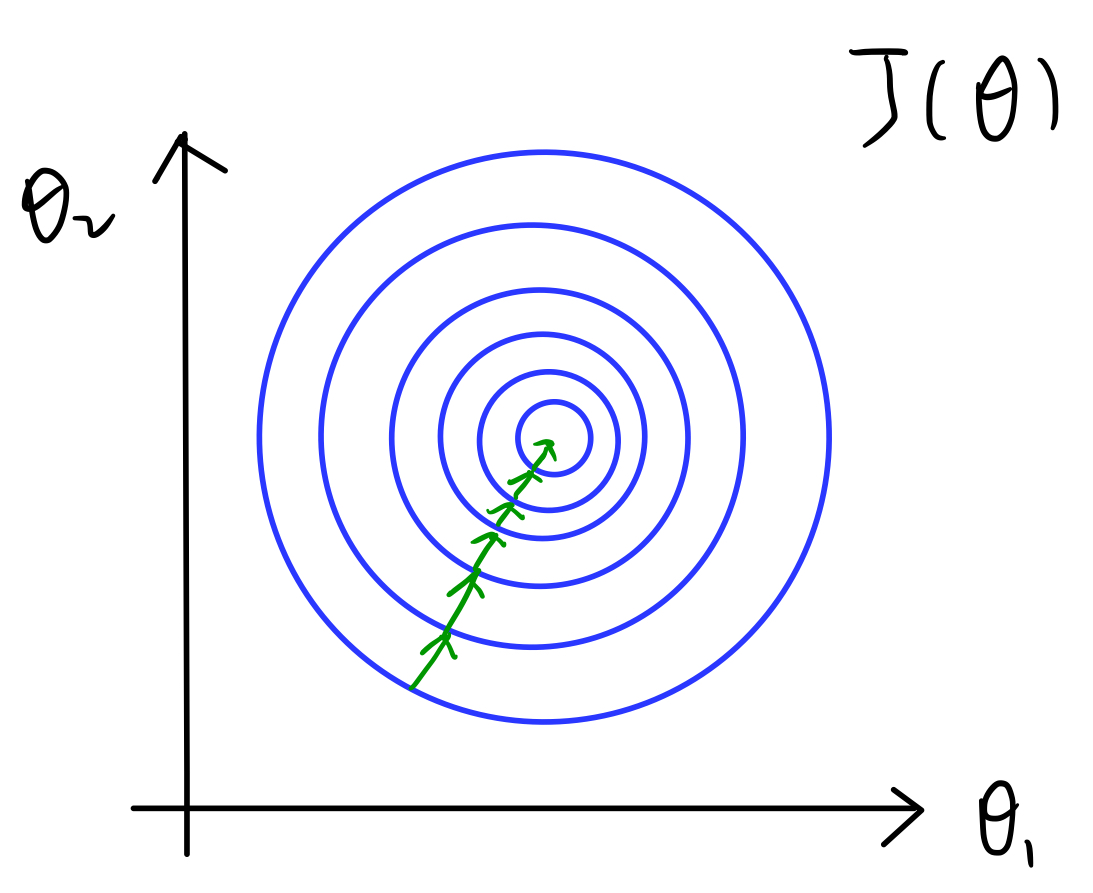
第二种情况,$x1\in\frac{[0,2000]}{2000}$,$x2\in\frac{[0,5]}{5}$。
这时候,我们的损失函数$J(\theta)$的轮廓图可能会变得更圆一些,这时候进行梯度下降就可以走更捷径的路线。
mean normalization:
对所有的$x_i$进行如下处理
处理后的$x_i^{new}\in[-1,1]$
当然左右边界和1是差不到一个数量级的时候也是可以接受的。否则还是要均值归一化一下。
Gradient Descent in Practice I-Learning Rate(吴恩达ML)
- 当学习率$\alpha$太小的时候:下降缓慢
当学习率$\alpha$太大的时候:并不是在每次迭代上都会下降。
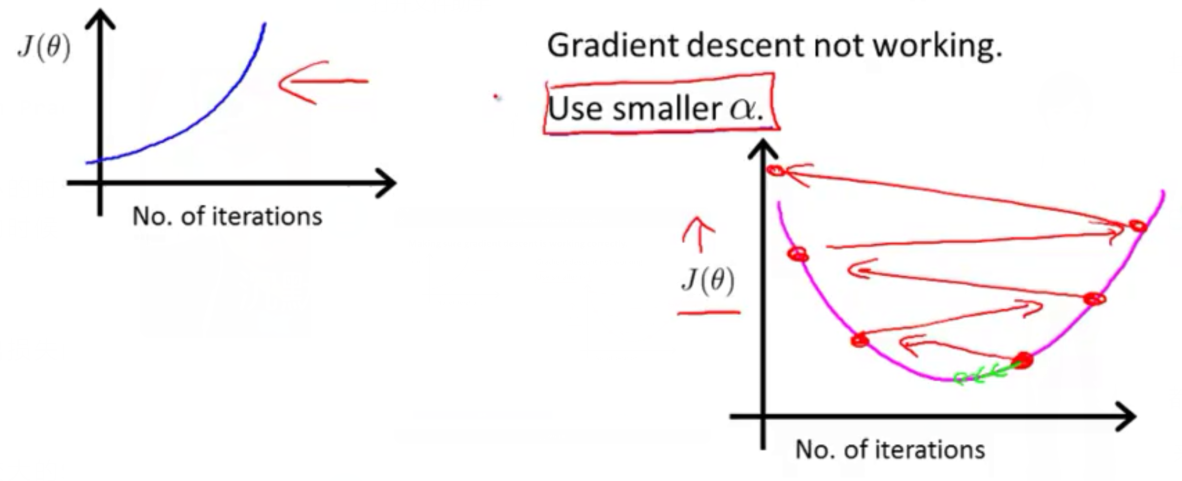
调参的时候,可以输出损失函数的下降曲线,来进行$\alpha$的选择;
刚开始的时候可以用较大的$\alpha$,后来可以用小的$\alpha$。