西瓜书笔记3 线性模型

基本形式

给定由n个属性描述的样例$\boldsymbol{x}=(x_1,x_2,…,x_n)$，其中$x_i$是$\boldsymbol{x}$在第i个属性上的取值。线性模型试图学得一个通过属性的线性组合来进行预测的函数，即

$$f(\boldsymbol{x})=w_1x_1+w_2x_2+...+w_nx_n+b$$

一般用向量形式表示

$$f(\boldsymbol{x})=\boldsymbol{w}^T\boldsymbol{x}+b$$

其中$\boldsymbol{w}=(w_1;w_2;…;w_n)$

$\boldsymbol{w}$和$b$学得后，模型就得以确认。

线性回归

最简单线性回归

给定数据集$D=\{(x_1,y_1),(x_2,y_2),…,(x_m,y_m)\}$。现试图学得

$$f(x_i)=wx_i+b, 使得f(x_i)\approx{y}_i$$

如何确定$w$和$b$呢？2.3节介绍过，均方误差是回归任务中最常用的性能度量。

$$E_{(w,b)}=\sum_{i=1}^m(f(x_i)-y_i)^2$$

最小化均方误差，即

$$(w^*,b^*)=\underset{(w,b)}{\arg\min}\sum_{i=1}^m(wx_i+b-y_i)^2$$

基于均方误差最小化进行模型求解的方法称为“最小二乘法”。
在线性回归中，最小二乘法就是试图找到一条直线，使所有样本到直线上的欧氏距离之和（均方误差）最小。

我们要求解$w$和$b$使得$E_{(w,b)}$最小。可将$E_{(w,b)}$分别对$w$和$b$求偏导，即

$$\frac{\partial{E_{(w,b)}}}{\partial{w}}=2(w\sum_{i=1}^mx^2_i-\sum_{i=1}^m(y_i-b)x_i)$$ $$\frac{\partial{E_{(w,b)}}}{\partial{b}}=2(mb-\sum_{i=1}^m(y_i-wx_i))$$

将偏导置零，可得到$w$和$b$的最优解的闭式解

$$w=\frac{\sum_{i=1}^my_i(x_i-\overline{x})}{\sum_{i=1}^mx^2_i-\frac{1}{m}(\sum_{i=1}^mx_i)^2}$$ $$b=\frac{1}{m}\sum_{i=1}^m(y_i-wx_i)$$

这里$E_{(w,b)}$是关于$w$和$b$的凸函数，当它导数均为0时，得到$w$和$b$的最优解。

二阶导数在区间上非负，则称为凸函数；若二阶导数在区间上恒大于0，则称为严格凸函数。

关于其他凸函数的数学知识，可参见《凸优论》

多元线性回归

给定数据集$D=\{(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),…,(\boldsymbol{x}_m,y_m)\}$，样本由m个属性描述。现试图学得

$$f(\boldsymbol{x}_i)=\boldsymbol{w}^T\boldsymbol{x}_i+b, 使得f(\boldsymbol{x}_i)\approx{y}_i$$

类似的，可用最小二乘法对$\boldsymbol{w}$和$b$进行估计。

为方便讨论，把$\boldsymbol{w}$和$b$吸收入向量形式$\hat{\boldsymbol{w}}=(\boldsymbol{w};b)$

把数据集$D$表示为一个$m\times(n+1)$大小的矩阵$X$

$$X=\begin{pmatrix} \boldsymbol{x}_1^T & 1\\ \boldsymbol{x}_2^T & 1\\ \vdots & \vdots\\ \boldsymbol{x}_m^T &1 \end{pmatrix}$$

再把标记也写成向量形式$\boldsymbol{y}=(y_1;y_2;...;y_m)$

均方误差

$$E_{\hat{\boldsymbol{w}}}=(\boldsymbol{y}-\boldsymbol{X}\hat{\boldsymbol{w}})^T(\boldsymbol{y}-\boldsymbol{X}\hat{\boldsymbol{w}})$$

最小二乘法（均方误差最小化）

$$\hat{\boldsymbol{w}}^*=\underset{\hat{\boldsymbol{w}}}{\arg\min}\ E_{\hat{\boldsymbol{w}}}$$

对$\hat{\boldsymbol{w}}$求导得

$$\frac{\partial{E}_{\hat{\boldsymbol{w}}}}{\partial{\hat{\boldsymbol{w}}}}=2\boldsymbol{X}^T(\boldsymbol{X}\hat{\boldsymbol{w}}-\boldsymbol{y})$$

同样，令导数为零可得$\hat{\boldsymbol{w}}$最优解的闭式解。

但由于涉及矩阵逆运算，比单变量要复杂一些。

当$\boldsymbol{X}^T\boldsymbol{X}$为满秩矩阵或正定矩阵时，令导数为零可得

$$\hat{\boldsymbol{w}}=(\boldsymbol{X}^T\boldsymbol{X})^{-1}\boldsymbol{X}^T\boldsymbol{y}$$

令$\hat{\boldsymbol{x}}_i=(\boldsymbol{x}_i;1)$，则最终的多元线性回归模型为

$$f(\hat{\boldsymbol{x}}_i)=\hat{\boldsymbol{x}}_i^T\hat{\boldsymbol{w}}$$

满秩矩阵：$秩=\min(行数,列数)$。

实对称矩阵：n阶矩阵；各元素为实数；$A^T=A$。

正定矩阵：实对称矩阵+对任意$\boldsymbol{X}\neq\boldsymbol{0}$，都有$\boldsymbol{X}^TA\boldsymbol{X}>0$。

广义线性模型：

现将$y$进行一个非线性映射到$g(y)$，再进行线性回归。

考虑单调可微函数$g(\cdot)$，使

$$g(y)=\boldsymbol{w}^T\boldsymbol{x}+b$$

则

$$y=g^{-1}(\boldsymbol{w}^T\boldsymbol{x}+b)$$

比如，假设我们认为示例所对应的输出标记实在指数尺度上变化，就可将输出标记的对数作为线性模型逼近目标，即

$$\ln y=\boldsymbol{w}^T\boldsymbol{x}+b$$

对数几率回归

上节讨论的是线性模型进行回归学习，但是如果是分类任务的话。

考虑二分类问题，线性回归模型产生的预测值$z=\boldsymbol{w}^T\boldsymbol{x}+b$是实值。

我们将$z$通过一个“Sigmoid函数”映射到（0,1）区间

$$y=\frac{1}{1+e^{-z}}$$

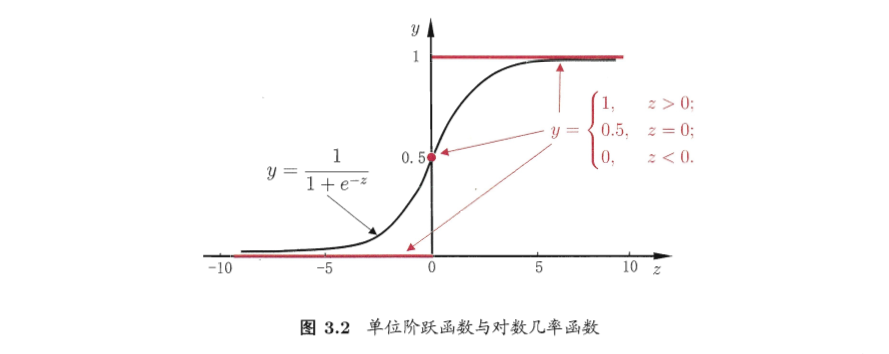
转化成线性模型就是

$$\ln\frac{y}{1-y}=\boldsymbol{w}^T\boldsymbol{x}+b$$

将y视为类后验概率估计$p(y=1|\boldsymbol{x})$，则上式可重写为

$$\ln\frac{p(y=1|\boldsymbol{x})}{p(y=0|\boldsymbol{x})}=\boldsymbol{w}^T\boldsymbol{x}+b$$

显然有

$$p(y=1|\boldsymbol{x})=\frac{e^{\boldsymbol{w}^T\boldsymbol{x}+b}}{1+e^{\boldsymbol{w}^T\boldsymbol{x}+b}} \tag{1}$$ $$p(y=0|\boldsymbol{x})=\frac{1}{1+e^{\boldsymbol{w}^T\boldsymbol{x}+b}} \tag{2}$$

于是，我们可通过“极大似然法”来估计$\boldsymbol{w}$和$b$。模型的对数似然为

$$\ell(\boldsymbol{w},b)=\sum_{i=1}^m\ln{p}(y_i|\boldsymbol{x}_i;\boldsymbol{w},b)$$

为便于讨论，令$\boldsymbol{\beta}=(\boldsymbol{w};b)$，$\hat{\boldsymbol{x}}=(\boldsymbol{x};1)$，则$\boldsymbol{w}^T\boldsymbol{x}+b$可简写为$\boldsymbol{\beta}^T\hat{\boldsymbol{x}}$

则对数似然可重写为

$$\ell(\boldsymbol{\beta})=\sum_{i=1}^m\ln(y_i\cdot{\color{Blue}{p(y=1|\hat{\boldsymbol{x}};\boldsymbol{\beta})}}+(1-y_i)\cdot{\color{Red}{p(y=0|\hat{\boldsymbol{x}};\boldsymbol{\beta})}})$$

$y_i=1$时，起作用的只有蓝色项的后验概率

$y_i=0$时，起作用的只有红色项的后验概率

根据（1）（2）式可知，最大化上式，等价于最小化

$$\ell(\boldsymbol{\beta})=\sum_{i=1}^m(-y_i\boldsymbol{\beta}^T\hat{\boldsymbol{x}}_i+\ln(1+e^{\boldsymbol{\beta}^T\hat{\boldsymbol{x}}_i}))$$

上式是关于$\boldsymbol{\beta}$的高阶可导连续凸函数，根据凸优化理论，经典的数值优化算法如梯度下降法、牛顿法都可求得其最优解。

$$\boldsymbol{\beta}^*=\underset{\boldsymbol{\beta}}{\arg\min}\ \ell(\boldsymbol{\beta})$$

线性判别分析

线性判别分析（Linear Discriminant Analysis，简称LDA）是一种监督学习的降维技术，也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。PCA是不考虑样本类别输出的无监督降维技术。
LDA的思想非常朴素：给定训练样例集，设法将样例投影到一条直线上使得同类样例的投影点尽可能近，异类样例的投影点尽可能远。

二分类LDA原理

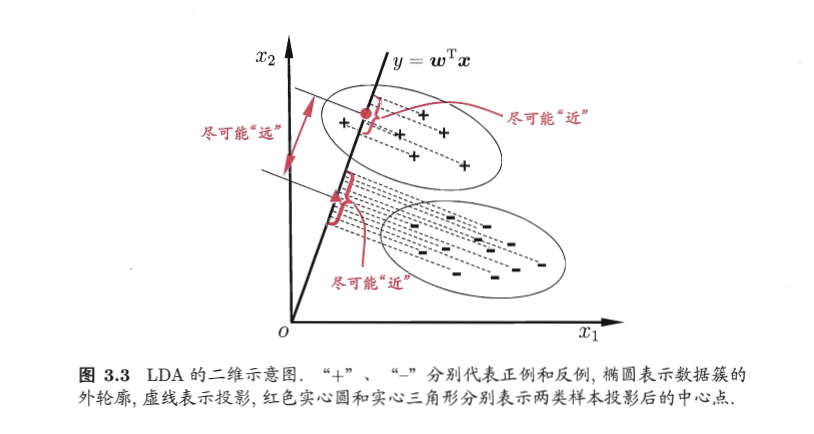
给定数据集$D=\{(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),…,(\boldsymbol{x}_m,y_m)\}$，$y_i\in\{0,1\}$，令$\boldsymbol{X}_i$、$\boldsymbol{\mu}_i$、$\boldsymbol{\Sigma}_i$分别表示第$i\in\{0,1\}$类示例的集合、均值向量、协方差矩阵。

将数据投影到直线$\boldsymbol{w}$上，则两类样本中心在直线上的投影分别为$\boldsymbol{w}^T\boldsymbol{\mu}_0$和$\boldsymbol{w}^T\boldsymbol{\mu}_1$；若将所有样本点都投影到直线上，则两类样本的协方差$\boldsymbol{w}^T\boldsymbol{\Sigma}_0\boldsymbol{w}$和$\boldsymbol{w}^T\boldsymbol{\Sigma}_1\boldsymbol{w}$。

投影后的协方差矩阵：

$$\begin{align*} & \quad\sum_{\boldsymbol{x}\in\boldsymbol{X}_0}(\boldsymbol{w}^T\boldsymbol{x}-\boldsymbol{w}^T\boldsymbol{\mu}_0)^2\\ & =\sum_{\boldsymbol{x}\in\boldsymbol{X}_0}(\boldsymbol{w}^T(\boldsymbol{x}-\boldsymbol{\mu}_0))^2\\ & =\sum_{\boldsymbol{x}\in\boldsymbol{X}_0}(\boldsymbol{w}^T(\boldsymbol{x}-\boldsymbol{\mu}_0)(\boldsymbol{x}-\boldsymbol{\mu}_0)^T\boldsymbol{w})\\ & =\boldsymbol{w}^T[\sum_{\boldsymbol{x}\in\boldsymbol{X}_0}(\boldsymbol{x}-\boldsymbol{\mu}_0)(\boldsymbol{x}-\boldsymbol{\mu}_0)^T]\boldsymbol{w}\\ & =\boldsymbol{w}^T\boldsymbol{\Sigma}\boldsymbol{w} \end{align*}$$

• 欲使同类样本的投影点尽可能近，可以让同类样本投影点的协方差尽可能小，即$\boldsymbol{w}^T\boldsymbol{\Sigma}_0\boldsymbol{w}+\boldsymbol{w}^T\boldsymbol{\Sigma}_1\boldsymbol{w}$尽可能小；
• 欲使异类样本投影点尽可能远，可以让类中心的距离尽可能大，即$||\boldsymbol{w}^T\boldsymbol{\mu}_0-\boldsymbol{w}^T\boldsymbol{\mu}_1||_2^2$尽可能大。

同时考虑二者，则得到欲最大化的目标

$$\begin{align*} & J=\frac{||\boldsymbol{w}^T\boldsymbol{\mu}_0-\boldsymbol{w}^T\boldsymbol{\mu}_1||^2_2}{\boldsymbol{w}^T\boldsymbol{\Sigma}_0\boldsymbol{w}+\boldsymbol{w}^T\boldsymbol{\Sigma}_1\boldsymbol{w}}\\ & \quad=\frac{\boldsymbol{w}^T(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)^T\boldsymbol{w}}{\boldsymbol{w}^T(\boldsymbol{\Sigma}_0+\boldsymbol{\Sigma}_1)\boldsymbol{w}} \tag{1} \end{align*}$$

• 定义“类内散度矩阵”（within-class scatter matrix） $$\boldsymbol{S}_{w}=\boldsymbol{\Sigma}_0+\boldsymbol{\Sigma}_1$$
• 定义“类间散度矩阵”（between-class scatter matrix） $$\boldsymbol{S}_{b}=(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)^T$$

则（1）式可重写为

$$J=\frac{\boldsymbol{w}^T\boldsymbol{S}_b\boldsymbol{w}}{\boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}} \tag{2}$$

这就是LDA欲最大化的目标，即$\boldsymbol{S}_b$和$\boldsymbol{S}_w$的“广义瑞利商”。

如何求解$\boldsymbol{w}$呢？注意到上式的分子和分母都是关于$\boldsymbol{w}$的二次项，因此（2）式的解与$\boldsymbol{w}$的长度无关，只与其方向有关。（若$\boldsymbol{w}$是一个解，则对于任意常数$\alpha$，$\alpha\boldsymbol{w}$也是一个解。）令$\boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}=1$，则问题转化为

$$\begin{align*} & \underset{\boldsymbol{w}}{\min}\quad-\boldsymbol{w}^T\boldsymbol{S}_b\boldsymbol{w}\\ & s.t.\quad\boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}=1\tag{3} \end{align*}$$

该问题的拉格朗日函数可写为

$$L(\boldsymbol{w},\lambda)=-\boldsymbol{w}^T\boldsymbol{S}_b\boldsymbol{w}+\lambda(\boldsymbol{w}^T\boldsymbol{S}_w\boldsymbol{w}-1)$$

对于等式约束$\lambda\in\mathbb{R}$

$$\frac{\partial{L}}{\partial\boldsymbol{w}}=-2\boldsymbol{S}_b\boldsymbol{w}+2\lambda\boldsymbol{S}_w\boldsymbol{w}$$

偏导数为0得

$$\boldsymbol{S}_b\boldsymbol{w}=\lambda\boldsymbol{S}_w\boldsymbol{w}$$

即

$$\boldsymbol{S}_w^{-1}\boldsymbol{S}_b\boldsymbol{w}=\lambda\boldsymbol{w}$$

通过特征值分解可得解

多分类LDA原理

• 定义“全局散度矩阵”

$$\begin{align*} \boldsymbol{S}_t& =\boldsymbol{S}_b+\boldsymbol{S}_w\\ & =\sum_{i=1}^m(\boldsymbol{x}_i-\boldsymbol{\mu})(\boldsymbol{x}_i-\boldsymbol{\mu})^T \end{align*}$$

• 重定义“类内散度矩阵”为每个类别的散度矩阵之和

$$\boldsymbol{S}_w=\sum_{i=1}^N\boldsymbol{S}_{w_i},$$

其中

$$\boldsymbol{S}_{w_i}=\sum_{\boldsymbol{x}\in\boldsymbol{X}_i}(\boldsymbol{x}-\boldsymbol{\mu}_i)(\boldsymbol{x}-\boldsymbol{\mu}_i)^T$$

• “类间散度矩阵”

$$\begin{align*} \boldsymbol{S}_b& =\boldsymbol{S}_t-\boldsymbol{S}_w\\ & =\sum_{i=1}^Nm_i(\boldsymbol{\mu}_i-\boldsymbol{\mu})(\boldsymbol{\mu}_i-\boldsymbol{\mu})^T \end{align*}$$

常见的一种实现是采用优化目标

$$\underset{\boldsymbol{W}}{\max}\frac{tr(\boldsymbol{W}^T\boldsymbol{S}_b\boldsymbol{W})}{tr(\boldsymbol{W}^T\boldsymbol{S}_w\boldsymbol{W})}$$

可通过如下广义特征值问题求解：

$$\boldsymbol{S}_b\boldsymbol{W}=\lambda\boldsymbol{S}_w\boldsymbol{W}$$

$\boldsymbol{W}$的闭式解则是$\boldsymbol{S}_w^{-1}\boldsymbol{S}_b$的$d’$个最大非零广义特征值所对应的特征向量组成的矩阵，$d’\leq{N-1}$。

LDA算法流程

输入：数据集$D=\{(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),…,(\boldsymbol{x}_m,y_m)\}$,其中任意样本$\boldsymbol{x}_i$为$n$维向量，$y_i∈\{C_1,C_2,…,C_k\}$，降维到的维度$d$。

输出：降维后的样本集$D′$

　　　　1) 计算类内散度矩阵$\boldsymbol{S}_w$

　　　　2) 计算类间散度矩阵$\boldsymbol{S}_b$

　　　　3) 计算矩阵$\boldsymbol{S}^{−1}_wS_b$

　　　　4）计算$S^{−1}_w\boldsymbol{S}_b$的最大的$d$个特征值和对应的$d$个特征向量$(w_1,w_2,…w_d)$，得到投影矩阵$W$

　　　　5) 对样本集中的每一个样本特征$\boldsymbol{x}_i$,转化为新的样本$\boldsymbol{z}_i=\boldsymbol{W}^T\boldsymbol{x}_i$
　　　　
　　　　6) 得到输出样本集$D′=\{(\boldsymbol{z}_1,y_1),(\boldsymbol{z}_2,y_2),…,(\boldsymbol{z}_m,y_m)\}$

多分类学习

考虑具有N个类别$C_1,C_2,…,C_N$的分类任务，多分类学习的基本思路是“拆分法”，即将多分类任务拆为若干个二分类任务求解。

最经典的查分策略有三种：

• 一对一（One vs. One，简称OvO）
• 一对余（One vs. Rest，简称OvR）
• 多对多（Many vs. Many，简称MvM）

OvO

给定数据集$D=\{(\boldsymbol{x}_1,y_1),…,(\boldsymbol{x}_m,y_m)\}$，$y_i\in\{C_1,C_2,…,C_N\}$
OvO将这N个类别两两配对，产生$N(N-1)/2$个分类器任务，最终结果可由投票产生

OvR

每次讲一个类作为正例、其他类的样例作为反例来训练N个分类器。
若有多个分类器预测为正类，则通常考虑各分类器的预测置信度。

MvM（&ECOC）

每次将若干个类作为正类，若干个其他类作为反。“纠错输出码”（Error Correcting Output Codes）是一种最常用的MvM技术。

ECOC是将编码的思想引入类别拆分，，并尽可能在解码过程中具有容错性。ECOC的工作过程主要分为两步：

• 编码：对N个类别做M次划分，每次划分将一部分类别划分为正类，一部分为反类，从而形成M个二分类任务。
• 【：M个分类器分别于测试样本进行预测，这些预测标记组成一个编码。将这个预测编码与各类别编码进行比较，返回距离最小的那个类别。

举个例子：

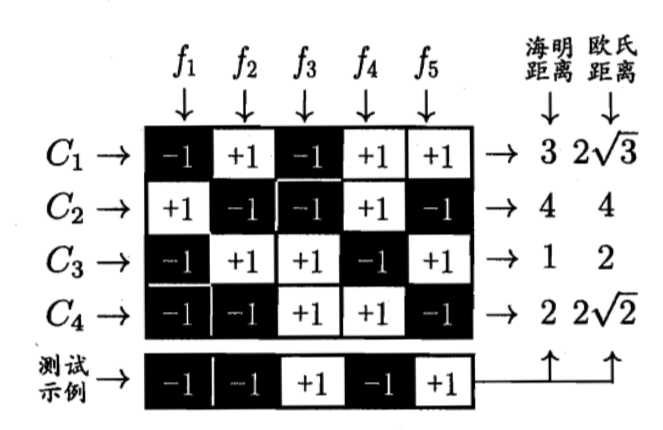
将四个类别$\{C_1,C_2,C_3,C_4\}$进行五次划分$\{f_1,f_2,f_3,f_4,f_5\}$，从而生成五个二分类任务。如，在任务$f_1$中，将$C_2$划分为正类，$C_1,C_3,C_4$划分为反类。五次划分后，$C_1$的编码为$(-1,+1,-1,+1,+1)$，可以明确地是，每个类的编码都是不同的。

现在讲一个测试样例在这五个分类器中，得出的编码为$(-1,-1,+1,-1,+1)$。五个类中与其距离最近的为$C_3$，所以被分类为$C_3$。

可以看出，每个类别的编码还是需要经过特殊设计的。

类别不平衡问题

前面介绍的分类学习方法都有一个共同的基本假设，即不同类别的训练样例数目相当。

我们在用$y=\boldsymbol{w}^T\boldsymbol{x}+b$对新样本$\boldsymbol{x}$进行分类时，用预测出的$y$值和一个阈值进行比较，通常$y>0.5$时判为正例，否则为反例。y实际上表达了正例的可能性，几率$\frac{y}{1-y}$则反映了正例可能性与反例可能性的比值。
阈值0.5对应的分类器决策规则为：

$$若\frac{y}{1-y}>1\quad则\ 预测为正例$$

当训练集中正、反例的数目不同时，$m^+$表示正例数目、$m^-$表示反例数目，则观测几率是$\frac{m^+}{m^-}$。只要分类器的预测几率高于观测几率就应判定为正例，即

$$若\frac{y}{1-y}>\frac{m^+}{m^-}\quad则\ 预测为正例$$

实际执行时使用“再缩放”进行决策

$$若\frac{y'}{1-y'}=\frac{y}{1-y}\times\frac{m^-}{m^+}>1\quad则\ 预测为正例$$