Logistic Regression on MNIST dataset

Posted on | In | Visitors:
Words count in article: 1.3k | Reading time ≈ 6
实现逻辑回归算法，并在MNIST数据集中查看学习器的效果。

Logistic-Regression-on-MNIST-dataset

目标：实现逻辑回归算法，并在MNIST数据集中查看学习器的效果。

Minist数据集

数据类别：手写数字数据集，有0~9这十个类别。每张图片是$28\times28\times1$的灰度图像。

image_1crc2rjnn18vv1e7bak573j1vca9.png-5.2kB

数据集规模：训练集为60000个样本，测试集为10000个样本。

由于有10个类，可以采用OvR的多分类处理，也可以采用EOCO编码来做MvM。

逻辑回归实现

逻辑回归模型

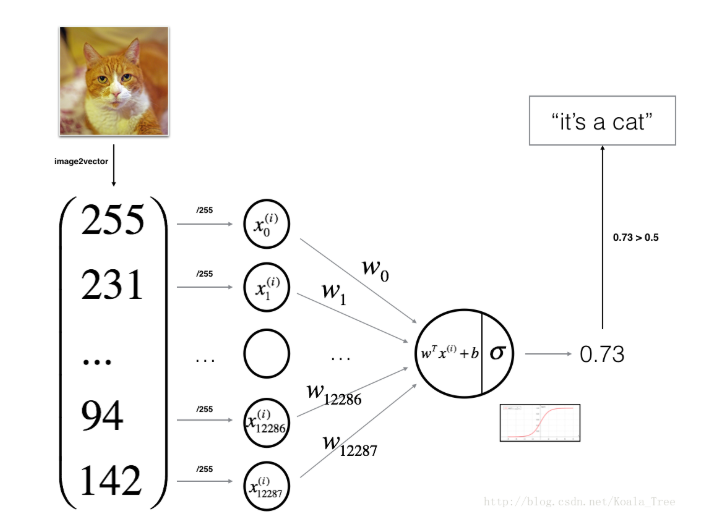
image_1crc33ceu1h5b15ns1vj212gj1j15m.png-95.8kB

逻辑回归算是个采用Sigmoid激活函数的神经网络单元了。

对于一个样例$\boldsymbol{x}_i$：

我们的模型包含两部分：线性部分和激活函数：

若$\hat{y}_i\leq0.5$，则为反例；若$\hat{y}_i>0.5$，则为正例。

$\hat{y}$可视该样例属于正类的概率。

损失函数

单个变量$\boldsymbol{x}_i$损失函数为（对数似然）：

当$y_i=0$时，即$\boldsymbol{x}_i$属于反类，对数损失为$\ln(1-\hat{y}_i)$；
当$y_i=1$时，即$\boldsymbol{x}_i$属于正类，对数损失为$\ln\hat{y}_i$。

对于所有训练样本的损失函数为

现在我们要的参数$(\boldsymbol{w}^{*},b^{*})$要满足

梯度下降

目的是：寻找最优参数$\boldsymbol{w}^{*}$和$b^{*}$，使得我们的目标函数$J$最小。

  • 初始化$\boldsymbol{w},b$为零
    对数函数是一个凸函数，初始化为任意值都可通过梯度下降找到最优解。
1
2
w = np.zeros((X_train.shape[0], 1))
b = 0

进行num_iterations次梯度下降：

  • 用当前的$\boldsymbol{w}$和$b$计算$\hat{\boldsymbol{y}}$
1
2
# 首先求出线性部分和激活函数
y_hat = sigmoid(np.dot(w.T, X_train) + b)
  • 计算损失函数: 
1
2
3
# 计算损失函数
cost = -1.0 / m_train * np.sum(Y_train * np.log(y_hat) + (1 - Y_train) * np.log(1 - y_hat))
cost = np.squeeze(cost)
  • 计算损失函数对w和b的偏导数
1
2
3
# 求梯度
dw = 1.0 / m_train * np.dot(X_train, (y_hat - Y_train).T)
db = 1.0 / m_train * np.sum(y_hat - Y_train)
  • 梯度下降获得新的w，b
1
2
3
# 梯度下降
w = w - learning_rate * dw
b = b - learning_rate * db

经过num_iterations次梯度下降就得到我们最后的$\boldsymbol{w}^{*}$和$b^{*}$了。
（当然不一定是完全收敛好的解，这些还需要我们去挑一些参数。）
将$\boldsymbol{w}^{*}$和$b^{*}$带入，就得到我们模型的最终的$\hat{\boldsymbol{y}}$

1
2
3
4
# 训练集上的predict y_hat
y_hat_train = sigmoid(np.dot(w.T, X_train) + b)
# 测试集上的predict y_hat
y_hat_test = sigmoid(np.dot(w.T, X_test) + b)

$\hat{\boldsymbol{y}}$算是属于正类的概率。
根据我们的阈值0.5，可以进一步的到最终的预测值（1表示正类，0表示反类）

1
2
3
4
y_prediction_train = np.zeros((1, m_train))
y_prediction_train[y_hat_train > 0.5] = 1
y_prediction_test = np.zeros((1, m_test))
y_prediction_test[y_hat_test > 0.5] = 1

总的模型函数如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
def model(X_train, Y_train, X_test, Y_test, num_iterations=2000, learning_rate=0.5, print_cost=False):
    """
    逻辑回归模型
    
    参数：
    X_train -- np数组(num_px * num_px, m_train)
    Y_train -- np数组(1, m_train)
    X_test -- np数组(num_px * num_px, m_test)
    Y_test -- np数组(1, m_test)
    num_iterations -- 超参数 迭代次数
    learning_rate -- 超参数 学习率
    print_cost -- Set to true to print the cost every 100 iterations
    
    """

    # 训练集样本数
    m_train = X_train.shape[1]
    # 测试集样本数
    m_test = X_test.shape[1]

    # 初始化w和b为0
    # w 权重, np数组(num_px * num_px, 1)
    w = np.zeros((X_train.shape[0], 1))
    b = 0

    # 新建一个数组,实时记录损失函数（我们的优化目标）,后面可以画出来看看梯度下降的效果
    costs = []
    # 进行num_iterations次迭代,每次迭代算一次梯度下降
    for i in range(num_iterations):
    
        # 首先求出线性部分和激活函数
        A = sigmoid(np.dot(w.T, X_train) + b)
        # 计算损失函数
        cost = -1.0 / m_train * np.sum(Y_train * np.log(A) + (1 - Y_train) * np.log(1 - A))  
        cost = np.squeeze(cost)
    
        # 求梯度
        dw = 1.0 / m_train * np.dot(X_train, (A - Y_train).T)
        db = 1.0 / m_train * np.sum(A - Y_train)
        
        # 梯度下降
        w = w - learning_rate * dw
        b = b - learning_rate * db

        # 记录一下损失
        if i % 100 == 0:
            costs.append(cost)
        
        # 每一百次迭代打印一次损失
        
        if print_cost and i % 100 == 0:
            print("Cost after iteration %i: %f" % (i, cost))

    w = w.reshape(-1, 1)
    
    # 训练集上的predict y_hat
    y_hat_train = sigmoid(np.dot(w.T, X_train) + b)
    # 测试集上的predict y_hat
    y_hat_test = sigmoid(np.dot(w.T, X_test) + b)
    # 训练集上的predict 类别
    y_prediction_train = np.zeros((1, m_train))
    y_prediction_train[y_hat_train > 0.5] = 1
    # 测试集上的predict 类别
    y_prediction_test = np.zeros((1, m_test))
    y_prediction_test[y_hat_test > 0.5] = 1

    d = {"costs": costs,
         "Y_prediction_test": y_prediction_test,
         "Y_prediction_train": y_prediction_train,
         "Y_hat_test": y_hat_test,
         "Y_hat_train": y_hat_train,
         "w": w,
         "b": b,
         "learning_rate" : learning_rate,
         "num_iterations": num_iterations}
    
    return d

导入MNIST数据集后，采用OvM的思想训练10个分类器。进行分类就可以了。

每个分类器都是一个类别为正例，另外九个类别为反例。
这样$正例:反例=1:9$，虽然正例数目远远小于反例数目，并不会产生类别不平衡的问题，因为这个比例大致就是数据的真实分布产生的比例。

完整代码见此处

-------------The End-------------