cs231n assignment1(SVM)

实验相关cs231n课程教程：Linear classification: Support Vector Machine, Softmax

这个实验是，用线性分类器SVM ，在CIFAR-10数据集上做图像分类。

关于CIFAR-10数据集的介绍，移步这里。
（！！此处应该有个超链接！！）

关于支持向量机SVM的介绍，移步这里。
（！！此处应该有个超链接！！）

线性模型

线性模型非常简单

$f(x_i, W, b) = x_iW+b$

对于CIFAR-10数据集来说，$x_i$的维度是$[1\times3072]$，$W$的维度是$[3072\times10]$，$b$是$[1\times10]$。

使用bias trick之后（参考课程教程），$x_i$的维度变为$[1\times3073]$，$W$变为$[3073\times10]$，模型如下。

$f(x_i, W) = Wx_i$

模型得到的是一个$[1\times10]$的分数矩阵，分数最高的类别就是学习器的预测结果。

多分类SVM的损失

对于样本$i$，类别$j$的得分为：$s_j=f(x_i,W)_j=(x_iW)_j$。样本$i$的损失为

$L_i=\sum_{j\neq{y_i}}\max(0, s_j-s_{y_i}+\Delta)$

这是SVM loss的目标是让样本的正确类别的得分要比错误类别的得分高至少$\Delta$。
HMDVZPP123KTP3.png-81.8kB

为不让超平面过拟合，引入正则化项，这里用L2正则化。

$R(W)=||W||^2$

总的损失就是这两部分之和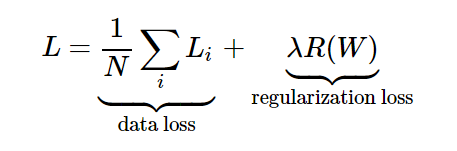

展开就是

$L=\frac{1}{m}\sum_{i}\sum_{j\neq{y_i}}[\max(0,w_j^Tx_i-w_{y_i}^Tx_i+\Delta)]+\lambda\sum_{k}\sum_{l}W_{k,l}^2$

损失的梯度推导

接下来就是优化了，采用最常用的梯度下降法。如果尝试课上讲的那种在计算图上求导感觉会有点乱。

正则化向的导数

$\frac{\partial{R}}{\partial{W_{k,l}}}=2W_{k,l}$

前面每个样本的的每个分类的得分损失

$\sum_{i}\sum_{j\neq{y_i}}\max(0,w_j^Tx_i-w_{y_i}^Tx_i+\Delta)$

可以看到有多个部分对$w_j^T$的导数都有贡献。$\frac{\partial{f}}{\partial{w^T_j}}=\sum_k\frac{\partial{f}}{\partial{p}_k}\cdot\frac{\partial{p_k}}{\partial{w^T_j}}$
对每个$L_{i,j},j\neq y_i$，有

$\frac{\partial{L_{i,j}}}{\partial{w^T_j}}=x_i$ $\frac{\partial{L_{i,j}}}{\partial{w^T_{y_i}}}=-x_i$

计算损失&梯度（code）

two_loops

two_loops的公式上文已经推出，下面是实现。

def svm_loss_naive(W, X, y, reg):
  """
  Structured SVM loss function, naive implementation (with two loops).

  Inputs have dimension D, there are C classes, and we operate on minibatches of N examples.

  Inputs:
  - W: A numpy array of shape (D, C) containing weights.
  - X: A numpy array of shape (N, D) containing a minibatch of data.
  - y: A numpy array of shape (N,) containing training labels; y[i] = c means
    that X[i] has label c, where 0 <= c < C.
  - reg: (float) regularization strength

  Returns a tuple of:
  - loss as single float
  - gradient with respect to weights W; an array of same shape as W
   """

  dW = np.zeros(W.shape) # initialize the gradient as zero

   # compute the loss and the gradient
  num_classes = W.shape[1]
  num_train = X.shape[0]
  loss = 0.0
  for i in range(num_train):
    scores = X[i].dot(W)
    correct_class_score = scores[y[i]]
    for j in range(num_classes):
      if j == y[i]:
        continue
      margin = scores[j] - correct_class_score + 1 # note delta = 1
      if margin > 0:
        loss += margin
        
        # calculate the dW, Sj - Syi + 1(j!=yi)
        dW[:,j] += X[i].T
        dW[:,y[i]] -= X[i].T

  loss /= num_train
  dW /= num_train

  # Add regularization to the loss.
  loss += reg * np.sum(W * W)
  # Add regularization to the dW.
  dW += 2 * reg * W

  return loss, dW

one_loop

def svm_loss_one_loop(W, X, y, reg):
  """
  Structured SVM loss function, vectorized implementation.

  Inputs and outputs are the same as svm_loss_naive.
  """
  loss = 0.0
  dW = np.zeros(W.shape) # initialize the gradient as zero

  num_classes = W.shape[1]
  num_train = X.shape[0]

  for i in range(num_train):
    scores = X[i].dot(W)
    correct_class_score = scores[y[i]]
    margin = scores - correct_class_score + 1
    margin[y[i]] = 0
    margin = np.maximum(0, margin)
    loss += np.sum(margin)

    margin[margin > 0] = 1
    num_pos = np.sum(margin)
    margin[y[i]] = -num_pos
    dW += X[i].reshape(-1, 1).dot(margin.reshape(1, -1))

  loss /= num_train
  dW /= num_train
  
  # regularization
  loss += reg * np.sum(W * W)
  dW += 2 * reg * W

  return loss, dW

no_loop

def svm_loss_vectorized(W, X, y, reg):
    """
    Structured SVM loss function, vectorized implementation.

    Inputs and outputs are the same as svm_loss_naive.
    """
    loss = 0.0
    dW = np.zeros(W.shape)  # initialize the gradient as zero

    num_classes = W.shape[1]
    num_train = X.shape[0]
    scores = X.dot(W)

    y_i = scores[(range(num_train), y)].reshape(-1, 1)
    margin = scores - y_i + 1
    margin[(range(num_train), y)] = 0
    margin = np.maximum(0, margin)
    # 计算损失
    loss += np.sum(margin)
    loss /= num_train
    # 计算梯度
    margin[margin > 0] = 1
    row_sum = np.sum(margin, axis=1)
    margin[(range(num_train), y)] = -row_sum
    dW = np.dot(X.T, margin) / num_train

    # regularization
    loss += reg * np.sum(W * W)
    dW += 2 * reg * W

    return loss, dW

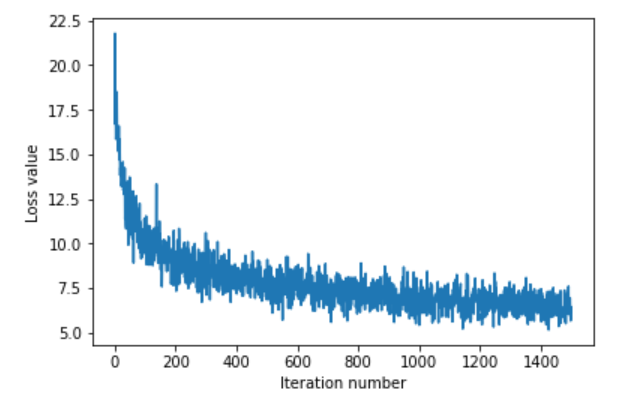
随机梯度下降

每次随机选一小部分mini_batch进行样本进行梯度下降。随机梯度下降的过程中，损失函数局部应该会有小的波动，但总体还是呈下降趋势。如图，

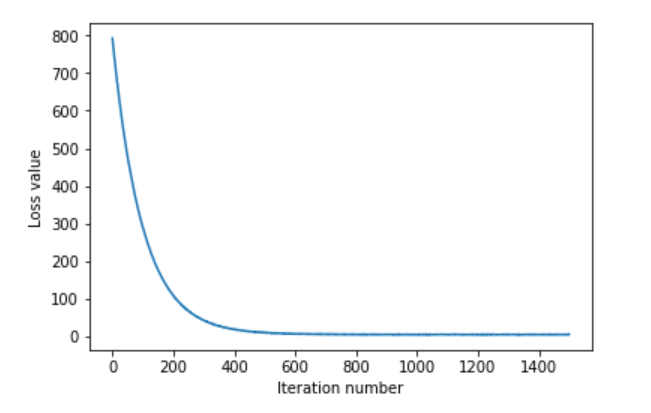
标准梯度下降，每次一定会下降。但是每次迭代对所有样本进行计算，计算量大。损失曲线比较平滑。如图，

np.random.choice(num, batch_size, replace=False)

在[0,num-1]中抽取batch_size个数字

replace=false表示不放回抽取。

线性分类器随机梯度下降的核心代码

loss_history = []
for it in range(num_iters):
     sample_index = np.random.choice(num_train, batch_size, replace=False)
    X_batch = X[sample_index, :]  # select the batch sample
    y_batch = y[sample_index]  # select the batch label

    # evaluate loss and gradient
    loss, grad = self.loss(X_batch, y_batch, reg)
    loss_history.append(loss)
    self.W += -learning_rate * grad

if verbose and it % 100 == 0:
    print('iteration %d / %d: loss %f' % (it, num_iters, loss))

return loss_history

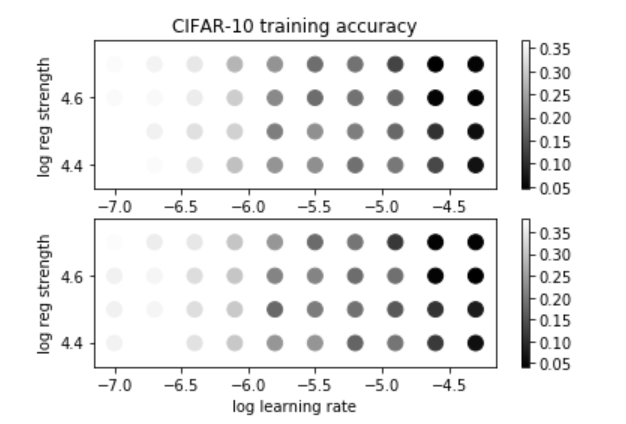
步长&正则化常数调参

步长的范围是$[1e-7,5e-5]$，一般是等比增加的；
正则化的范围是$[2.5e4,5e4]$，这里采用等差增加。
最后在validation中的分数大概是0.38。（据说用心调可以到0.4左右，大概多取些值耐心等吧）

learning_rates = [1e-7, 5e-5]
regularization_strengths = [2.5e4, 5e4]

results = {}
best_val = -1   
best_svm = None 

# chooses the best hyperparameters by tuning on the validation 
learning_rates = np.log10(learning_rates)
for lr in np.logspace(learning_rates[0], learning_rates[1], 10):
    print("now padding: " + str(lr))
    for reg in np.linspace(regularization_strengths[0], regularization_strengths[1], 4):
        print("now_reg:" + str(reg))
        svm = LinearSVM()
        loss_hist = svm.train(X_train, y_train, learning_rate=lr, reg=reg,
                      num_iters=500, verbose=True)
        y_train_pred = svm.predict(X_train)
        y_val_pred = svm.predict(X_val)
        train_acc = np.mean(y_train == y_train_pred)
        val_acc = np.mean(y_val == y_val_pred)
        results[(lr, reg)] = (train_acc, val_acc)
        if val_acc > best_val:
            best_val = val_acc
            best_svm = svm

# Print out results.
for lr, reg in sorted(results):
    train_accuracy, val_accuracy = results[(lr, reg)]
    print('lr %e reg %e train accuracy: %f val accuracy: %f' % (lr, reg, train_accuracy, val_accuracy))
    
print('best validation accuracy achieved during cross-validation: %f' % best_val)

结果看一下图吧。
（上图训练集结果；下图验证集结果）
fjsaojgojefjsa.png-68.7kB