cs231n assignment1(Softmax)

Posted on | In | Visitors:
Words count in article: 2.8k | Reading time ≈ 11

cs231n assignment1(Softmax)

实验相关cs231n课程教程：Linear classification: Support Vector Machine, Softmax

这个实验是，用线性分类器Softmax ，在CIFAR-10数据集上做图像分类。

关于CIFAR-10数据集的介绍，移步这里。
（！！此处应该有个超链接！！）

上篇SVM实验介绍过线性模型，这里不再赘述。cs231n_assignment1(SVM)

多分类Softmax的损失

SVM是最常用的两个分类器之一，而另一个就是Softmax分类器，它的损失函数与SVM的损失函数不同。Softmax分类器就可以理解为逻辑回归分类器面对多个分类的一般化归纳。

softmax函数及损失

SVM将输出$f(x_i,W)$作为每个分类的评分。与SVM不同，Softmax的输出（归一化的分类概率）更加直观，并且从概率上可以解释。在Softmax分类器中，函数映射$f(x_i;W)=Wx_i$保持不变，但将这些评分值视为每个分类的未归一化的对数概率，并且将hinge loss替换为交叉熵损失cross-entropy loss。公式如下：

等价于下式

在上式中，使用$f_j$来表示分类评分向量$f$中的第$j$个元素，

其中$f_i(z)=\frac{e^{z_j}}{\sum_ke^{z_k}}$被称作softmax函数。可以看出通过这样处理之后，元素大小的单调性没有改变，每个元素被压缩到0~1之间，且所有元素的和为1。

数据集上的损失，和之前一样，就是数据集中所有样本数据的损失值$L_i$的均值与正则化损失$R(W)$之和。

信息理论解释

在经验分布$p$和估计分布$q$之间的交叉熵定义如下：

因此，Softmax分类器所做的就是最小化在估计分类概率（就是上面的$\frac{e^{f_{y_i}}}{\sum_je^{f_j}}$）和经验分布之间的交叉熵。

交叉熵还可以写成熵和相对熵（Kullback-Leibler divergence）

因为$H(p)$是固定的（我们是要优化$q$，使交叉熵最小），于是最小化交叉熵等价于最小化相对熵。即让$q$和$p$越相似越好，交叉熵最小化的终极目标，想让预测分布的所有概率密度都在正确分类上。

信息论相关知识，可移步：信息论基础

概率论解释

先看下面的公式：

我们的softmax函数可看为$x_i$正确分类的后验概率。

从概率论的角度来理解，我们就是在最小化正确分类的负对数概率，这可以看做是在进行最大似然估计（MLE）。

该解释的另一个好处是，损失函数中的正则化部分R(W)可以被看做是权重矩阵W的高斯先验，这里进行的是最大后验估计（MAP）而不是最大似然估计。

最大似然估计相关知识，可移步：最大似然估计

最大后验概率相关知识，可移步：最大后验概率
(= = 欠一个超链接 = =)

实操事项：数值稳定

编程实现softmax函数计算的时候，中间项$e^{f_{y_i}}$和$\sum_j e^{f_j}$因为存在指数函数，所以数值可能非常大。除以大数值可能导致数值计算的不稳定，所以学会使用归一化技巧非常重要。如果在分式的分子和分母都乘以一个常数$C$，并把它变换到求和之中，就能得到一个从数学上等价的公式：

$C$的值可自由选择，不会影响计算结果，通过使用这个技巧可以提高计算中的数值稳定性。通常将$C$设为 $logC=-max_jf_j$。代码实现如下：

1
2
3
4
5
6
f = np.array([123, 456, 789]) # 例子中有3个分类，每个评分的数值都很大
p = np.exp(f) / np.sum(np.exp(f)) # 数值问题，可能导致数值爆炸

# 那么将f中的值平移到最大值为0：
f -= np.max(f) # f becomes [-666, -333, 0]
p = np.exp(f) / np.sum(np.exp(f)) # 现在OK了，将给出正确结果

Softmax分类器的命名是从softmax函数那里得来的，softmax函数将原始分类评分变成正的归一化数值，所有数值和为1，这样处理后交叉熵损失才能应用。
注意从技术上说“softmax loss”是没有意义的，因为softmax只是一个压缩数值的函数。但是在这个说法常常被用来做简称。

损失的梯度推导

有了SVM的梯度推导经验，Softmax应该不太难。

正则化向的导数

with_loops梯度推导

前面每个样本的得分损失

前一项求导比较简单，只对$w_{y_i}^T$有贡献。

后一项对$W$的每一项$w_k^T$都有贡献。通过链式求导可得出

no_loop梯度推导

上面求导数过程是把 Loss 对于 W 的导数显示的写出来，然后直接对 W 求导数，在这个简单的例子中可以这样，但是一旦网络变得复杂了，就很难直接写出Loss 对于要求的表达式的导数了。
一种比较好的方式是利用链式法则逐级的求导数：

对于一个样本向量$x_i$

$L_i$对$f_j$的导数为

改写成向量形式，$L_i$对$f$的导数为

由$f=x_iW$可已看出，$f$对$W$的导数为

根据链式法则，可知

m个样本的情况

（其中MaskMat矩阵[i, y_i]位置为1，其他位置为0）

计算损失&梯度（code）

with_loops

with_loops的公式上文已经推出，下面是实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
def softmax_loss_naive(W, X, y, reg):
  """
  Softmax loss function, naive implementation (with loops)

  Inputs:
  - W: A numpy array of shape (D, C) containing weights.
  - X: A numpy array of shape (N, D) containing a minibatch of data.
  - y: A numpy array of shape (N,) containing training labels; y[i] = c means
    that X[i] has label c, where 0 <= c < C.
  - reg: (float) regularization strength

  Returns a tuple of:
  - loss as single float
  - gradient with respect to weights W; an array of same shape as W
  """
  # Initialize the loss and gradient to zero.
  loss = 0.0
  dW = np.zeros_like(W)
  
  num_train = X.shape[0]
  for i in range(num_train):
      # 初试分数
      scores = np.dot(X[i], W)
      # 加一个常数C
      scores -= np.max(scores)
      # softmax函数
      prob = np.exp(scores) / np.sum(np.exp(scores))
      # 计算损失
      loss += -np.log(prob[y[i]])
      # 前一项求导
      dW[:,y[i]] -= X[i].T
      # 后一项求导
      dW += np.dot(X[i].reshape(-1,1), prob.reshape(1,-1))

  loss /= num_train
  dW /= num_train
  # Regularization
  loss += reg * np.sum(W * W)
  dW += 2 * reg * W

  return loss, dW

no_loop

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def softmax_loss_vectorized(W, X, y, reg):
  """
  Softmax loss function, vectorized version.

  Inputs and outputs are the same as softmax_loss_naive.
  """
  # Initialize the loss and gradient to zero.
  loss = 0.0
  dW = np.zeros_like(W)
 
  num_train = X.shape[0]
  num_classes = W.shape[1]

  # 初试分数
  scores = np.dot(X, W)
  # 加一个常数C
  scores -= np.max(scores, axis=1, keepdims=True)
  # softmax函数
  prob = np.exp(scores) / np.sum(np.exp(scores), axis=1, keepdims=True)
  # 计算损失
  loss += -np.sum(np.log(prob[(range(num_train), y)]))
  # 预处理：前一项+到后一项中
  prob[(range(num_train),y)] += -1
  # 求梯度
  dW += np.dot(X.T, prob)

  loss /= num_train
  dW /= num_train

  # Regularization
  loss += reg * np.sum(W * W)
  dW += 2 * reg * W

  return loss, dW

步长&正则化常数调参

（这一部分和SVM几乎一样）

步长的范围是$[1e-7,5e-5]$，一般是等比增加的；
正则化的范围是$[2.5e4,5e4]$，这里采用等差增加。
最后在validation中的分数大概是0.349。（据说用心调可以到0.35左右）

代码不贴了，几乎一样的。

SVM和Softmax的比较

SVM分类器使用的是折叶损失hinge loss;
softmax分类器使用的是交叉熵损失corss-entropy loss。

分值解释不同

下图是针对一个数据点，SVM和Softmax分类器的不同处理方式的一个例子。

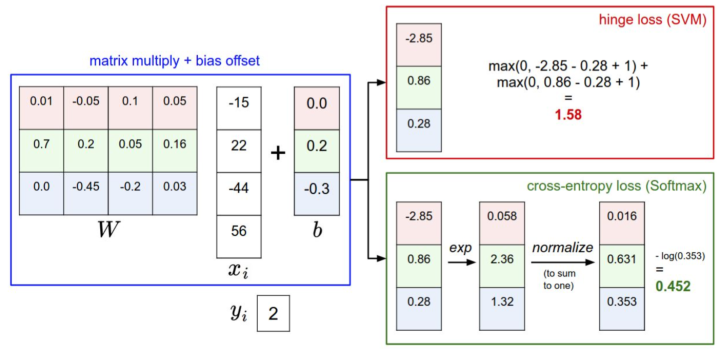
a90ce9e0ff533f3efee47473053820hd.png-112.4kB

两个分类器都计算了同样的分值向量$f$（本节中是通过矩阵乘来实现）。不同之处在于对$f$中分值的解释：

  • SVM分类器将它们看做是分类评分，它的损失函数鼓励正确的分类（本例中是蓝色的类别2）的分值比其他分类的分值高出至少一个边界值。
  • Softmax分类器将这些数值看做是每个分类没有归一化的对数概率，鼓励正确分类的归一化的对数概率变高，其余的变低。

Softmax分类器为每个分类提供了“可能性”：SVM的计算是无标定的，而且难以针对所有分类的评分值给出直观解释。Softmax分类器则不同，它允许我们计算出对于所有分类标签的可能性。

“可能性”分布的集中或离散程度是由正则化参数λ直接决定的。

举个例子，假设3个分类的原始分数是$[1,-2,0]$，那么softmax函数就会计算：

$[1,-2,0]\to[e^1,e^{-2},e^0]=[2.71,0.14,1]\to[0.7,0.04,0.26]$

现在，如果正则化参数λ更大，那么权重$W$就会被惩罚的更多，然后他的权重数值就会更小。这样算出来的分数也会更小，假设小了一半吧$[0.5,-1,0]$，那么softmax函数的计算就是：

$[0.5,-1,0]\to[e^{0.5},e^{-1},e^0]=[1.65,0.73,1]\to[0.55,0.12,0.33]$

现在看起来，概率的分布就更加分散了。

随着正则化参数λ不断增强，权重数值会越来越小，最后输出的概率会接近于均匀分布。

优化方向不同

考虑一个评分是[10, -2, 3]的数据，其中第一个分类是正确的。

  • 那么一个SVM（$\Delta=1$）会看到正确分类相较于不正确分类，已经得到了比边界值还要高的分数，它就会认为损失值是0。SVM对于数字个体的细节是不关心的：如果分数是[10, -100, -100]或者[10, 9, 9]，对于SVM来说没设么不同，只要满足超过边界值等于1，那么损失值就等于0。
  • 对于softmax分类器，情况则不同。对于[10, 9, 9]来说，计算出的损失值就远远高于[10, -100, -100]的。
  • 换句话来说，softmax分类器对于分数是永远不会满意的：正确分类总能得到更高的可能性，错误分类总能得到更低的可能性，损失值总是能够更小。但是，SVM只要边界值被满足了就满意了，不会超过限制去细微地操作具体分数。
-------------The End-------------