常用隐层激活函数
常见的隐藏单元激活函数如下:
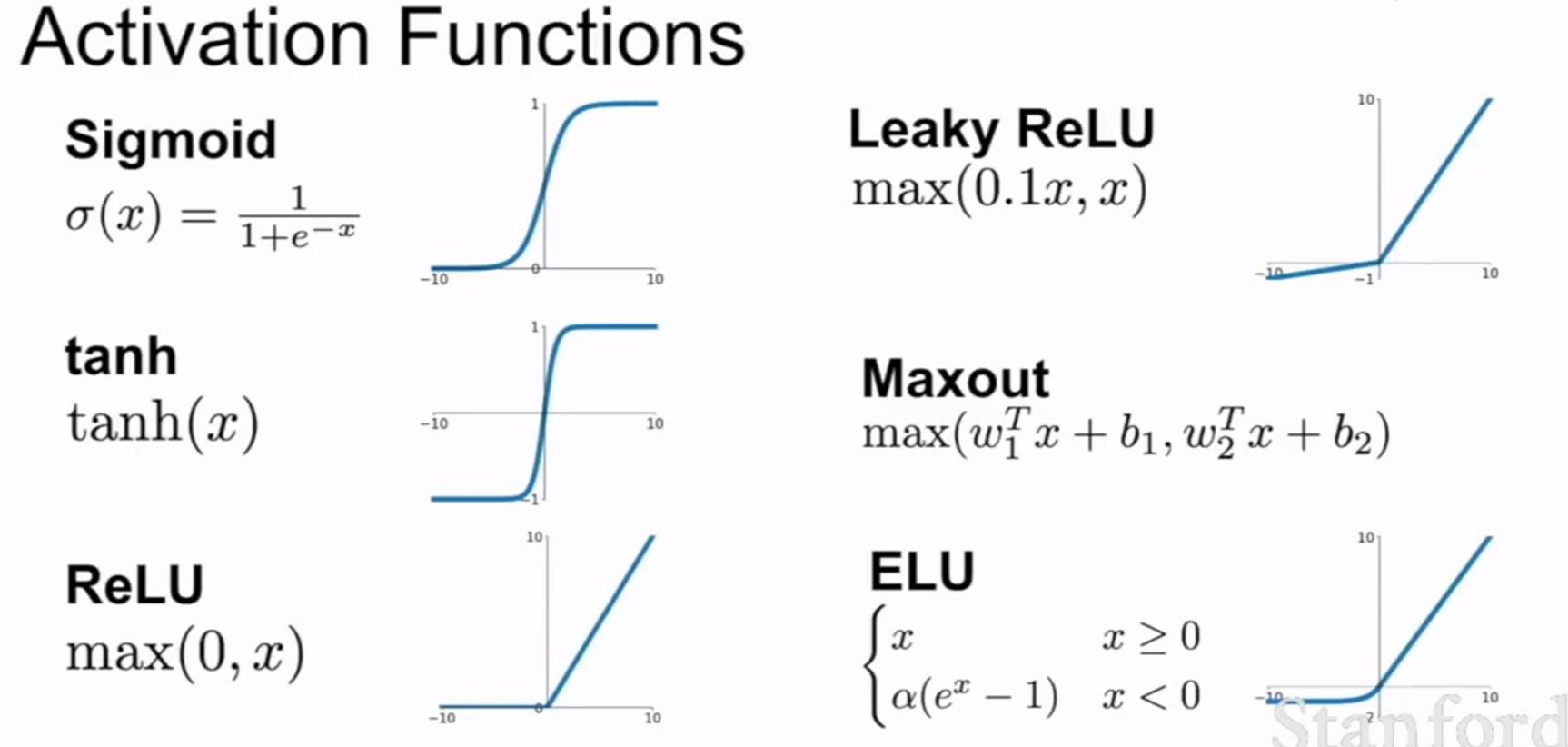
Sigmoid
Sigmoid将输入的实数值“挤压”到0到1范围内:

在历史上,sigmoid函数非常常用,这是因为它对于神经元的激活频率有良好的解释:从完全不激活(0)到在求和后的最大频率处的完全饱和(saturated)的激活(1)。
然而现在Sigmoid函数因为其两个主要缺点,实际已经很少使用了。
缺点:
- Sigmoid函数饱和,使梯度消失
Sigmoid函数在其大部分定义域内都饱和(Z绝对值很大),只有输入接近0,它们才对输入强烈敏感。
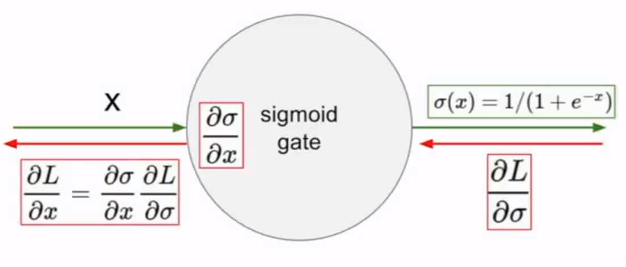
如图,在反向传播的时候,$\frac{\partial{\sigma}}{\partial{x}}$将会与整个损失函数关于该门单元输出的梯度(即$\frac{\partial{L}}{\partial{\sigma}}$)相乘。因此,如果局部梯度非常小,那么相乘的结果也会接近零,这会有效地“杀死”梯度,几乎就有没有信号通过神经元传到权重再到数据了。
- Sigmoid函数的输出不是零中心的
这一情况将影响梯度下降的运作,因为如果输入神经元的数据总是正数(比如在$f=w^Tx+b$中每个元素都$x>0$),那么关于$w$的梯度在反向传播的过程中,将会要么全部是正数,要么全部是负数(具体依整个表达式$f$而定)。这将会导致梯度下降权重更新时出现Z字型的下降。
但Sigmoid常作为二值型的输出单元,将$z=\boldsymbol{w}^T\boldsymbol{h}+b$转化成概率。
Tanh
注意tanh神经元是一个简单放大的sigmoid神经元,具体说来就是:
tanh将实数值压缩到[-1,1]之间:

和sigmoid神经元一样,它也存在饱和问题,但是和sigmoid神经元不同的是,它的输出是零中心的。因此,在实际操作中,tanh非线性函数比sigmoid非线性函数更受欢迎一些。
ReLU
极好的默认选择!!
简单来说,ReLU就是一个关于0的阈值:
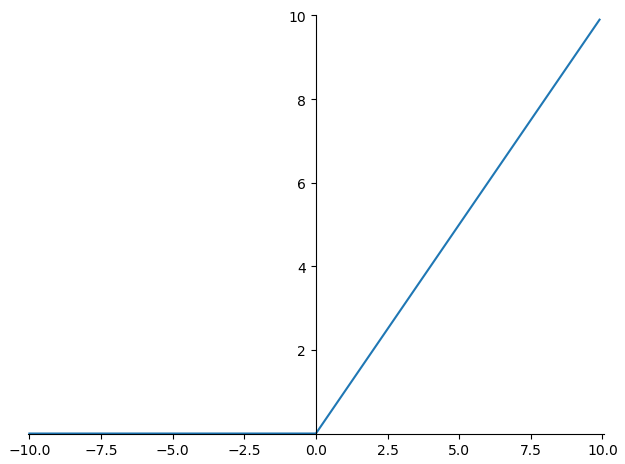
使用ReLU有以下一些优缺点:
优点:
- 收敛速度快
相较于sigmoid和tanh函数,ReLU对于随机梯度下降的收敛有巨大的加速作用( Krizhevsky 等的论文指出有6倍之多)。据称这是由它的线性,非饱和的公式导致的。 - 计算速度快
sigmoid和tanh神经元含有指数运算等耗费计算资源的操作,而ReLU可以简单地通过对一个矩阵进行阈值计算得到。
缺点:
- 在训练的时候,ReLU单元比较脆弱并且可能“died”。
举例来说,当一个很大的梯度流过ReLU的神经元的时候,可能会导致梯度更新到一种特别的状态,在这种状态下神经元将无法被其他任何数据点再次激活。如果这种情况发生,那么从此所以流过这个神经元的梯度将都变成0。也就是说,这个ReLU单元在训练中将不可逆转的死亡,因为这导致了数据多样化的丢失。
例如,如果学习率设置得太高,可能会发现网络中40%的神经元都会死掉(在整个训练集中这些神经元都不会被激活)。通过合理设置学习率,这种情况的发生概率会降低。
当初始化参数的时候,可以将$b$设置成一个小的正值,例如0.1。这会使ReLU很可能初始化时就对训练集中的大多数输入呈现激活状态,并且允许导数通过。
Leaky ReLU
其中$\alpha$是一个小的常量,例如0.01。
Leaky ReLU是为解决“ReLU死亡”问题的尝试。ReLU中当x<0时,函数值为0。而Leaky ReLU则是给出一个很小的负数梯度值,比如0.01。

有些研究者的论文指出这个激活函数表现很不错,但是其效果并不是很稳定。
Kaiming He等人在2015年发布的论文Delving Deep into Rectifiers中介绍了一种新方法PReLU,把负区间上的斜率当做每个神经元中的一个参数。然而该激活函数在在不同任务中均有益处的一致性并没有特别清晰。
Maxout
Maxout是对ReLU和leaky ReLU的一般化归纳。
这样Maxout神经元就拥有ReLU单元的所有优点(线性操作和不饱和),而没有它的缺点(死亡的ReLU单元)。
然而和ReLU对比,它每个神经元的参数数量增加了一倍,这就导致整体参数的数量激增。
总结
在同一个网络中混合使用不同类型的神经元是非常少见的,虽然没有什么根本性问题来禁止这样做。
那么该用那种呢?
用ReLU非线性函数。注意设置好学习率,监控网络中死亡的神经元占的比例;
如果单元死亡问题困扰你,就试试Leaky ReLU或者Maxout;
不要再用sigmoid了,也可以试试tanh,但是其效果应该不如ReLU或者Maxout。