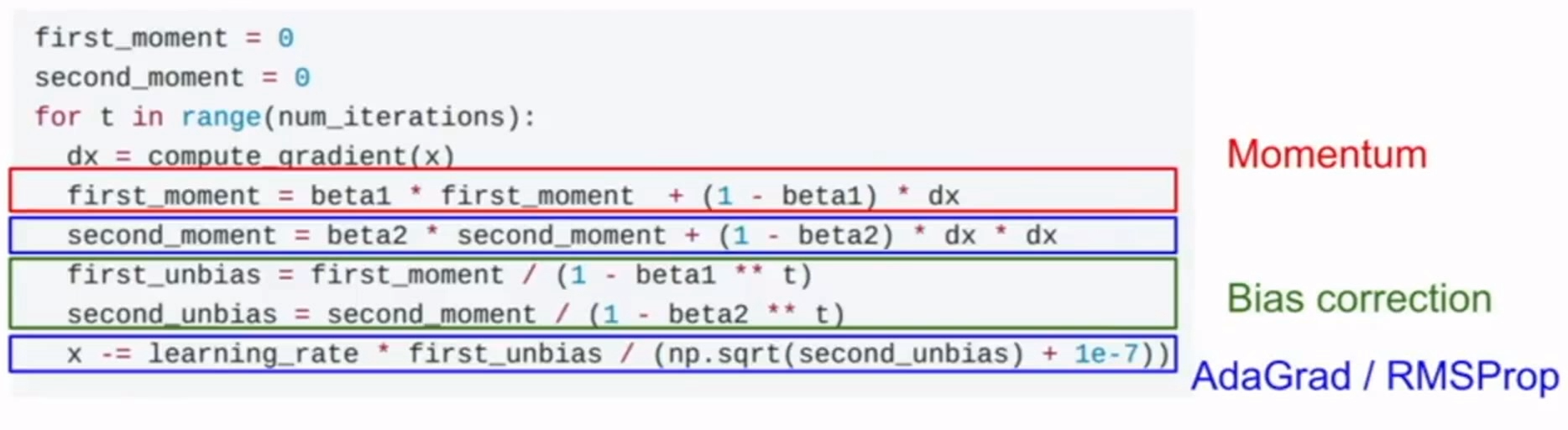
优化算法

指数加权平均数

我想向你展示几个优化算法，它们比梯度下降法快，要理解这些算法，你需要用到指数加权平均（Exponentially weighted averages），在统计中也叫做指数加权移动平均

下面是某地一年中（时间-温度）的散点图。

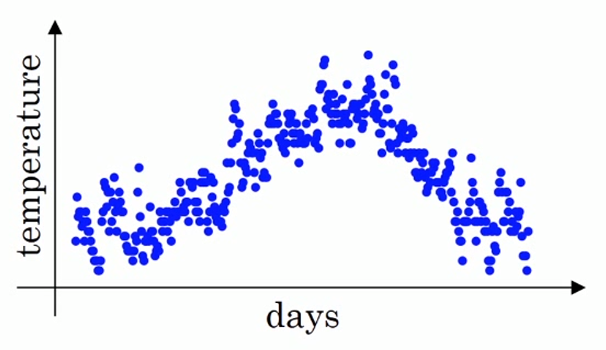
如果要计算趋势的话，也就是温度的局部平均值（或者说移动平均值）。

首先使$v_0=0$，每天需要使用$0.9$的加权数之前的数值加上当日温度$\theta_t$的0.1 倍，即

$v_t=0.9v_{t-1}+0.1\theta_t$

用红线表示该平均值，便得到这样的结果。

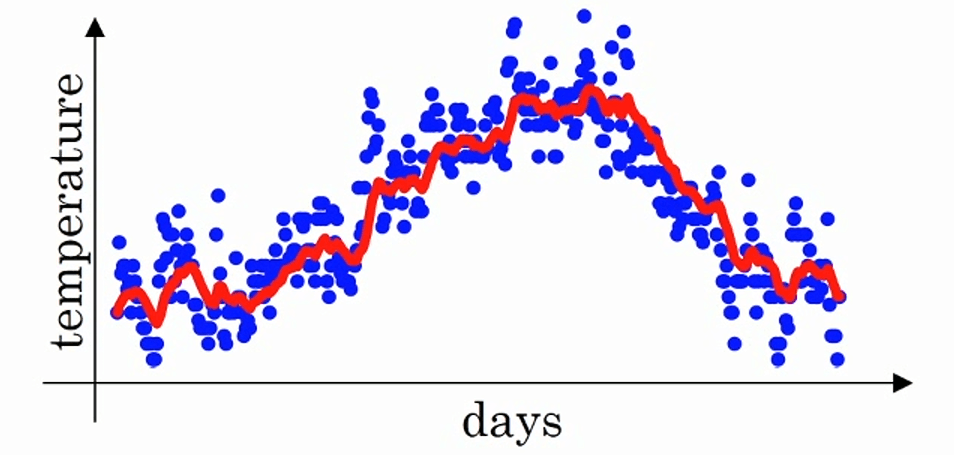
我们把$0.9$这个常数变成$\beta$，将之前的$0.1$变成$(1-\beta)$，得到移动平均值的一般形式

$v_t=\beta{v}_{t-1}+(1-\beta)\theta_t$

可将$v_t$大概视为前$\frac{1}{1-\beta}$天的平均温度

例如$\beta=0.9$，$v_t$（上图红线部分）约为前10天的平均值。
例如$\beta=0.98$，$v_t$（绿线部分）约为前50天的平均值。温度变化时，温度上下起伏小。

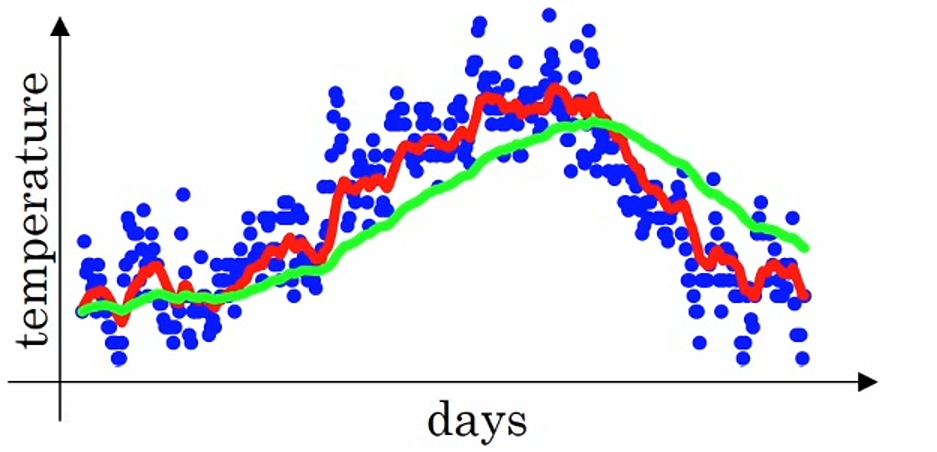
再例如$\beta=0.5$，$v_t$（黄线部分）约为前2天的平均值。温度变化时，温度上下起伏大。

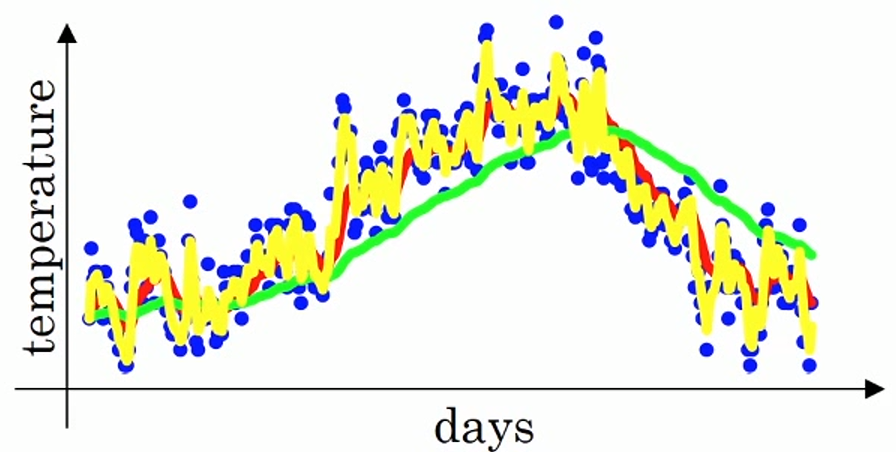
为什么可视为前$\frac{1}{1-\beta}$天的平均？

下图为$\beta=0.9$是，前i天的温度在$v_t$中所占的比例

由于
$\lim_{x\mapsto0}(1-x)^{\frac{1}{x}}=\frac{1}{e}$
这个例子中：10天后，$\theta_{t-i}$在$v_t$中所占的比例就不足$\theta_t$的$\frac{1}{e}$倍了，所以认为$v_t$约为近10天的平均温度。

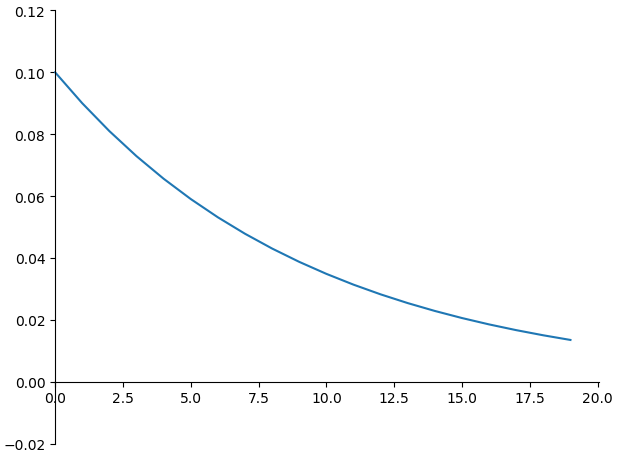
偏差修正

$\frac{v_t}{1-\beta^t}$

上文中，这个红色的线对应于$\beta=0.9$，绿色的线对应于$\beta=0.98$。

但如果执行的是这个公式的话，得到的$v_t$实际是紫色的线。

$v_t=0.9v_{t-1}+0.1\theta_t$

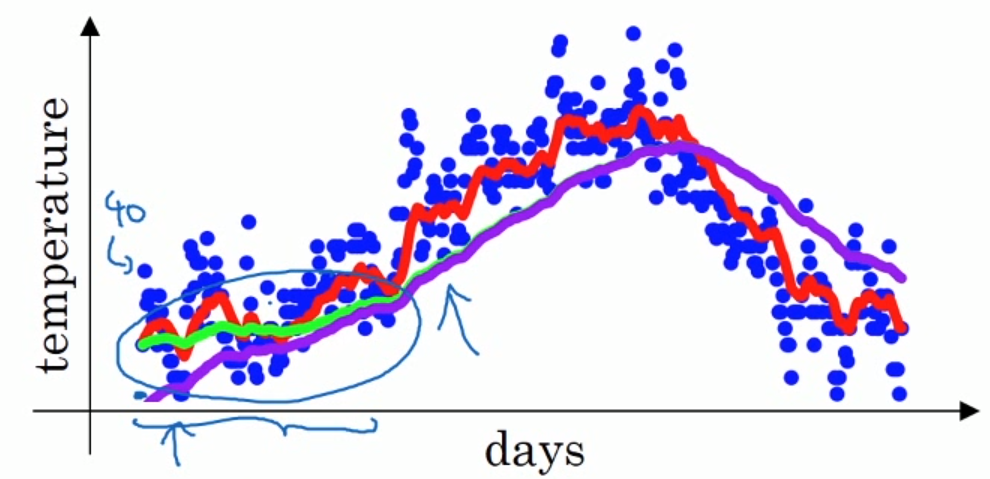
原因是我们初始化$v_0=0$，那么$v_1=0.98v_0+0.02\theta_1=0.02\theta_1$。所以对第一天的估计要小很多。

偏差修正可以修改这一估测，让估测变得更准确，特别是在估测初期，也就是不用$v_t$，而是用$\frac{v_t}{1-\beta^t}$，$t$是当前的天数。

动量梯度下降

Momentum

普通的梯度下降

1 2	# 普通更新 w += -learning_rate * dw

动量更新则是计算梯度的指数加权平均数，并利用该梯度进行更新

$\begin{align*} & v_{dW}=\beta{v}_{dW}+(1-\beta)dW\\ & W=W-\alpha*v_{dW} \end{align*}$

想象在一个碗状的函数上进行优化，某个位置的梯度是该点的加速度，梯度影响速度，速度再影响位置。（在普通更新中，梯度直接影响位置。）

1
2
3

# 动量更新
v = mu * v - learning_rate * dw # 梯度影响速度
w += v # 速度影响位置

在这里引入了一个初始化为0的变量v和一个超参数mu。mu在最优化的过程中被看做动量（一般值设为0.9），但其物理意义与摩擦系数更一致。这个变量有效地抑制了速度，降低了系统的动能，不然质点在山底永远不会停下来。

通过交叉验证，mu通常设为[0.5,0.9,0.95,0.99]中的一个。

通过动量更新，参数向量会在任何有持续梯度的方向上增加速度。

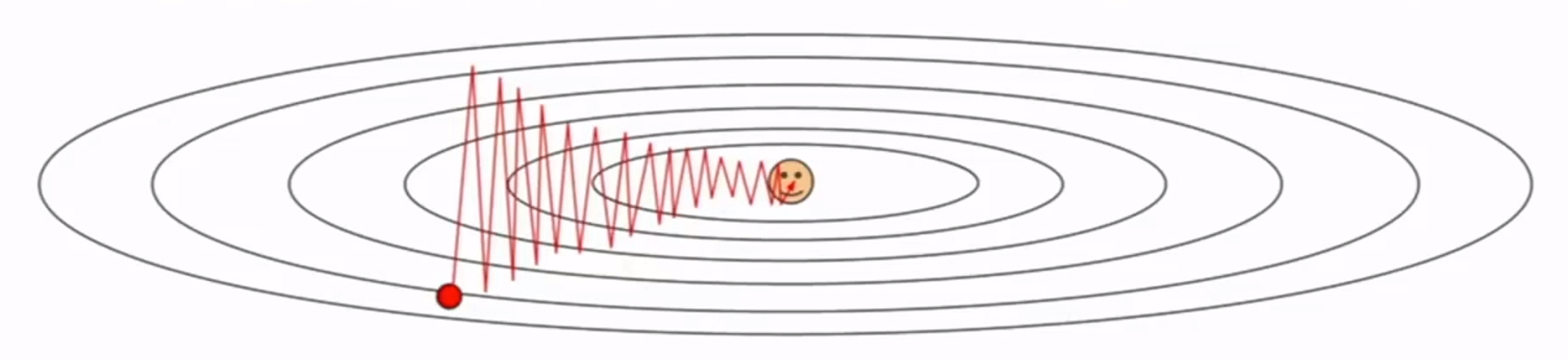
fjagjalihg.png-215.3kB

例如在上图中，普通SGD更新如图所示；而动量更新，方向上下变化的梯度在速度上变化不大，而持续向右的梯度方向，则可使速度持续向右增加，从而更快的下降。

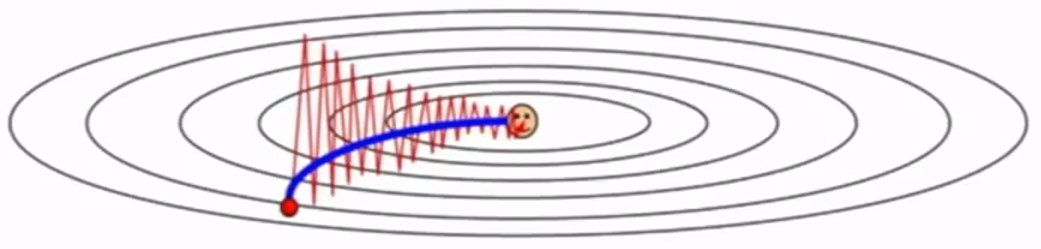
fasgjkahgfsd.png-177kB

陷入极小点和鞍点是普通梯度下降法可能遇到的不好的情况。而动量下降，可以使在到达极小点和鞍点时，按惯性“冲出”这种不好的情况。(即使没有梯度，仍会有速度)

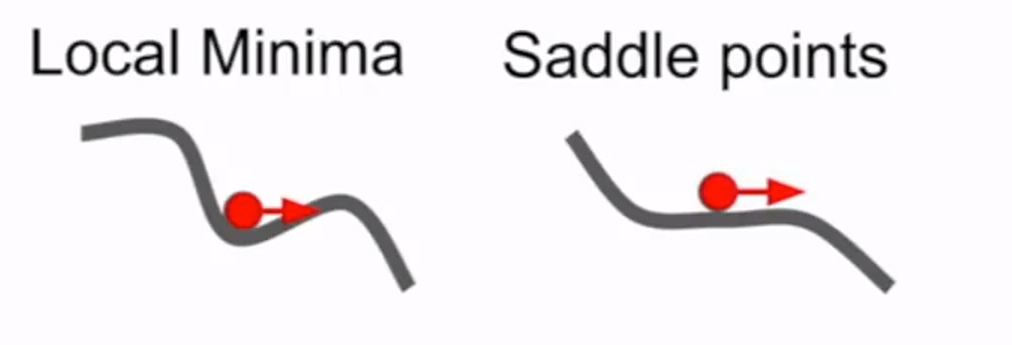
Nesterov Momentum

Nesterov动量的核心思路是，当参数向量位于某个位置$x$时，观察上面的动量更新公式可以发现，动量部分（忽视带梯度的第二个部分）会通过mu*v稍微改变参数向量。因此，如果要计算梯度，那么可以将未来的近似位置x+mu*v看做是“向前看”，这个点在我们一会儿要停止的位置附近。因此，计算x + mu * v的梯度而不是“旧”位置x的梯度就有意义了。

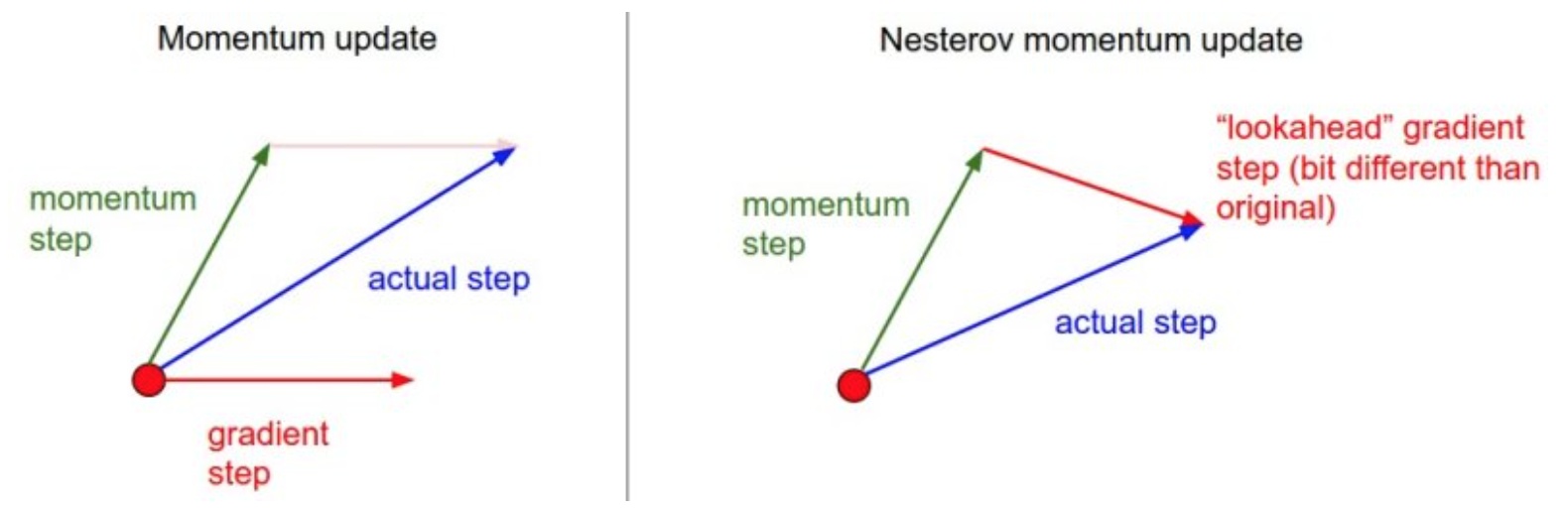
如图，既然我们知道动量将会把我们带到绿色箭头指向的点，我们就不要在原点（红色点）那里计算梯度了。使用Nesterov动量，我们就在这个"looked-ahead"的地方计算梯度。

$\begin{align*} & v_{t+1}=\beta{v}_t-\alpha\nabla{f}(w_t+\beta{v}_t)\\ & w_{t+1}=w_t+v_{t+1} \end{align*}$

x_ahead = x + mu * v
# 计算dx_ahead(在x_ahead处的梯度，而不是在x处的梯度)
v = mu * v - learning_rate * dx_ahead
x += v

令$\tilde{x}_t=x_t+\beta{v}_t$，就有另一个简单点的表示

$\begin{align*} & v_{t+1}=\beta{v}_t-\alpha\nabla{f}(\tilde{w}_t)\\ & \tilde{w}_{t+1}=\tilde{w}_t-\beta{v}_t+(1+\beta)v_{t+1} \end{align*}$

1
2
3

v_prev = v # 存储备份
v = mu * v - learning_rate * dx # 速度更新保持不变
x += -mu * v_prev + (1 + mu) * v # 位置更新变了形式

来自cs231n：
在理论上Nesterov Momentum对于凸函数它能得到更好的收敛，在实践中也确实比标准动量表现更好一些。

对于NAG（Nesterov’s Accelerated Momentum）的来源和数学公式推导，我们推荐以下的拓展阅读：

Yoshua Bengio的Advances in optimizing Recurrent Networks，Section 3.5。
Ilya Sutskever’s thesis (pdf)在section 7.2对于这个主题有更详尽的阐述。

Adagrad

Adagrad是一个由Duchi等提出的适应性学习率算法

1
2
3

# 假设有梯度和参数向量x
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

注意，变量cache跟踪了每个参数的梯度的平方和，用来归一化参数更新步长。cache使接收到高梯度值的权重更新的效果被减弱，而接收到低梯度值的权重的更新效果将会增强。

fjagjalihg.png-215.3kB

例如，这种情况下，纵向梯度值较高被，横向梯度较低，纵向梯度被削弱就会少走一些弯路。

eps（一般设为1e-4到1e-8之间）防止出现除以0的情况。

缺点：随着梯度的累计，步长会越来越小，容易陷入极小点，在深度学习中单调的学习率被证明通常过于激进且过早停止学习。

RMSprop

RMSprop是Adagrad的一种变体。

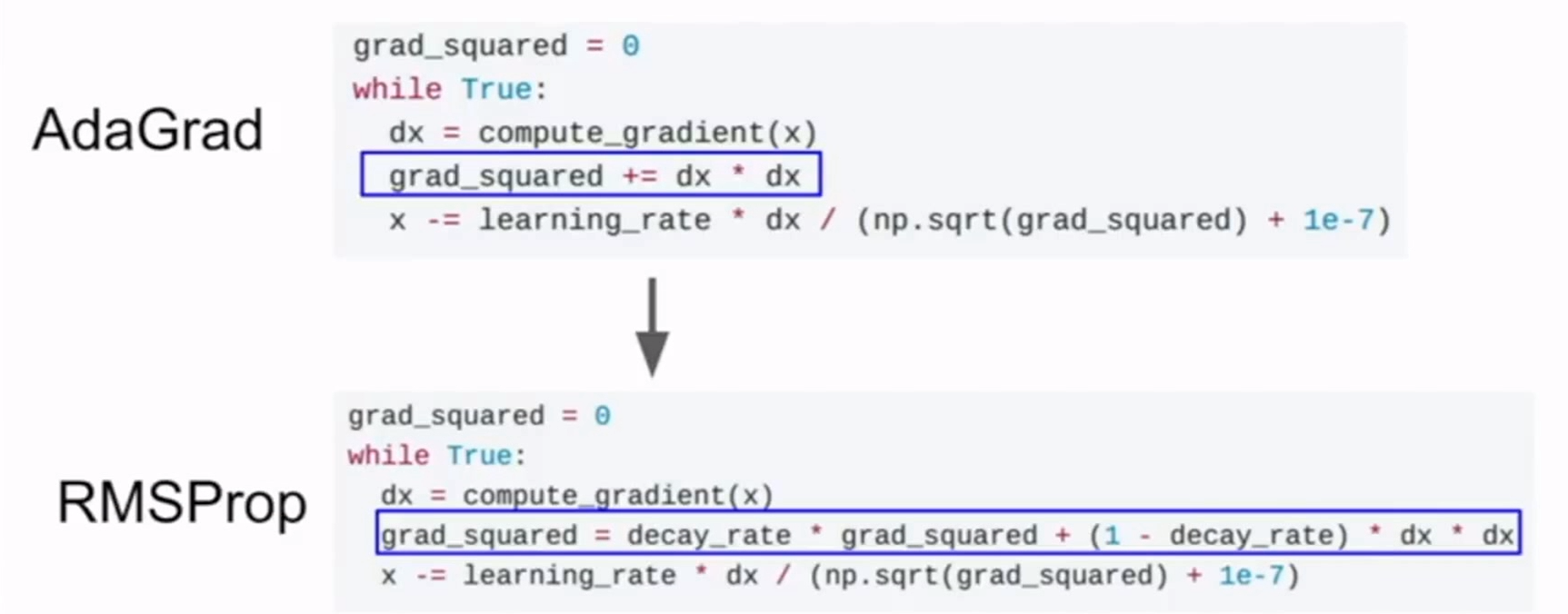
RMSprop将grad_squard作为梯度平方的指数加权平均。

1 2	cache = decay_rate * cache + (1 - decay_rate) * dx*2 x += - learning_rate dx / (np.sqrt(cache) + eps)

在上面的代码中，decay_rate是一个超参数，常用的值是[0.9,0.99,0.999]。

RMSProp仍然是基于梯度的大小来对每个权重的学习率进行修改，同样效果不错。但是和Adagrad不同，其更新不会让学习率单调变小。

Adam

Adam是最近才提出的一种更新方法，它看起来像是RMSProp的动量版。

简易版Adam：

image_1ct28nnkfl1l1fi0lla1rb2aj1m.png-327.3kB

注意这个更新方法看起来是RMSProp+Momentum。
论文中推荐的参数值eps=1e-8，beta1=0.9，beta2=0.999
（learning_rate=1e-3或5e-4）。
（在实际操作中，推荐Adam作为默认的算法，一般而言跑起来比RMSProp要好一点。但是也可以试试SGD+Nesterov动量。）

完整的Adam算法包含一个偏置修正机制，因为m，v两个矩阵初始为0，指数加权平均中，初期前存在较大偏差：就算梯度很小，也很可能会产生很大的步长。

完整版Adam：

image_1ct2915981t551eqr1r6lurv2tq13.png-520kB