cs231n assignment2(FullyConnectedNets)

Posted on | In | Visitors:
Words count in article: 1.2k | Reading time ≈ 6
层的模块化；更多优化算法

cs231n assignment2(FullyConnectedNets)

层的模块化

在assignment1中的实验中，曾经实现了一个two-layers-net。用的方法，一个公式一个公式的写出来的，当网络规模变大，就不好实现，重用性也差。本节实验就将层进行模块化，每一层都会实现一个forward和backward的函数。

例如一个forward函数

1
2
3
4
5
6
7
8
9
10
def layer_forward(x, w):
  """ Receive inputs x and weights w """
  # Do some computations ...
  z = # ... some intermediate value
  # Do some more computations ...
  out = # the output

  cache = (x, w, z, out) # Values we need to compute gradients

  return out, cache

例如一个backward函数

1
2
3
4
5
6
7
8
9
10
11
12
13
def layer_backward(dout, cache):
  """
  Receive dout (derivative of loss with respect to outputs) and cache,
  and compute derivative with respect to inputs.
  """
  # Unpack cache values
  x, w, z, out = cache

  # Use values in cache to compute derivatives
  dx = # Derivative of loss with respect to x
  dw = # Derivative of loss with respect to w

  return dx, dw

实现完各种层的forward和backward函数之后，就可以把他们进行组装，来实现不同解构的网络了。

Affine layer: forward

Affine layer是全连接层，前向传播就是

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def affine_forward(x, w, b):
    """
    Computes the forward pass for an affine (fully-connected) layer.

    The input x has shape (N, d_1, ..., d_k) and contains a minibatch of N
    examples, where each example x[i] has shape (d_1, ..., d_k). We will
    reshape each input into a vector of dimension D = d_1 * ... * d_k, and
    then transform it to an output vector of dimension M.

    Inputs:
    - x: A numpy array containing input data, of shape (N, d_1, ..., d_k)
    - w: A numpy array of weights, of shape (D, M)
    - b: A numpy array of biases, of shape (M,)

    Returns a tuple of:
    - out: output, of shape (N, M)
    - cache: (x, w, b)
    """
    out = None
    ###########################################################################
    # TODO: Implement the affine forward pass. Store the result in out. You   #
    # will need to reshape the input into rows.                               #
    ###########################################################################
    N = x.shape[0]
    D = w.shape[0]

    out = np.dot(x.reshape(N, D), w) + b
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    cache = (x, w, b)
    return out, cache

Affine layer: backward

根据链式法则

注意一下维度就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def affine_backward(dout, cache):
    """
    Computes the backward pass for an affine layer.

    Inputs:
    - dout: Upstream derivative, of shape (N, M)
    - cache: Tuple of:
      - x: Input data, of shape (N, d_1, ... d_k)
      - w: Weights, of shape (D, M)
      - b: Biases, of shape (M,)

    Returns a tuple of:
    - dx: Gradient with respect to x, of shape (N, d1, ..., d_k)
    - dw: Gradient with respect to w, of shape (D, M)
    - db: Gradient with respect to b, of shape (M,)
    """
    x, w, b = cache
    N = x.shape[0]
    D = w.shape[0]
    ###########################################################################
    # TODO: Implement the affine backward pass.                               #
    ###########################################################################
    dx = np.dot(dout, w.T).reshape(x.shape)
    dw = np.dot(x.reshape(N, D).T, dout)
    db = np.dot(np.ones((1, N)), dout).flatten()
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx, dw, db

ReLU layer: forward

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def relu_forward(x):
    """
    Computes the forward pass for a layer of rectified linear units (ReLUs).

    Input:
    - x: Inputs, of any shape

    Returns a tuple of:
    - out: Output, of the same shape as x
    - cache: x
    """
    ###########################################################################
    # TODO: Implement the ReLU forward pass.                                  #
    ###########################################################################
    out = np.maximum(0, x)
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    cache = x
    return out, cache

ReLU layer: backward

根据链式求导

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def relu_backward(dout, cache):
    """
    Computes the backward pass for a layer of rectified linear units (ReLUs).

    Input:
    - dout: Upstream derivatives, of any shape
    - cache: Input x, of same shape as dout

    Returns:
    - dx: Gradient with respect to x
    """
    dx, x = None, cache
    ###########################################################################
    # TODO: Implement the ReLU backward pass.                                 #
    ###########################################################################
    dx = dout
    dx[x <= 0] = 0
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx

Two-layer network

有了之前实现的模块，实现一个两层网络就比较简单。贴一下关键代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# forward
A1, cache1 = affine_relu_forward(X, W1, b1)
scores, cache2 = affine_forward(A1, W2, b2)

# If y is None then we are in test mode so just return scores
if y is None:
    return scores

# loss
loss, dscores = softmax_loss(scores, y)
loss += 0.5 * self.reg * (np.sum(W1 * W1) + np.sum(W2 * W2))
# backward
dA1, dW2, db2 = affine_backward(dscores, cache2)
dX, dW1, db1 = affine_relu_backward(dA1, cache1)

Multilayer network

实现一个如下结构的多层网络

{affine - relu} x (L - 1) - affine - softmax

关键代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# A0 = X
A = X
L = self.num_layers

# forward
for i in range(1, L):
    Z, params['cache1'+str(i)] = affine_forward(A, self.params['W'+str(i)], self.params['b'+str(i)])
    A, params['cache3'+str(i)] = relu_forward(Z)
scores, cache = affine_forward(A, self.params['W'+str(L)], self.params['b'+str(L)])

# If test mode return early
if mode == 'test':
    return scores
# cal the loss
loss, dscores = softmax_loss(scores, y)
sum_W_norm = 0.0
for i in range(self.num_layers):
    sum_W_norm += np.sum(self.params['W'+str(i+1)]**2)
loss += 0.5 * self.reg * sum_W_norm
# backward
dA, grads['W'+str(L)], grads['b'+str(L)] = affine_backward(dscores, cache)
for i in range(L-1, 0, -1):
    dZ = relu_backward(dA, params['cache3'+str(i)])
    dA, grads['W'+str(i)], grads['b'+str(i)] = affine_backward(dZ, params['cache1' + str(i)])
for i in range(L):
    grads['W'+str(i+1)] += self.reg * self.params['W'+str(i+1)]

另外，初始化的时候注意，W是weight_scale*标准高斯分布的随机数。

优化方法

公式及笔记参见：优化方法（more）

SGD+Momentum

关键代码

1
2
v = config['momentum'] * v - config['learning_rate'] * dw
next_w = w + v

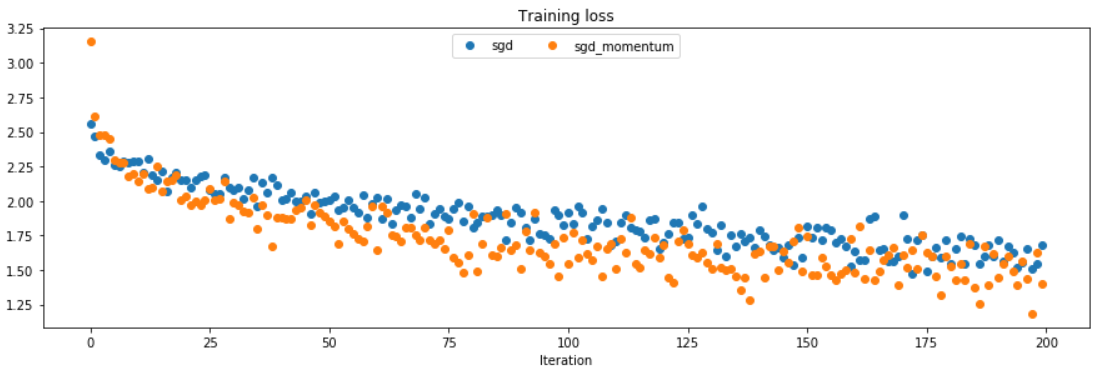
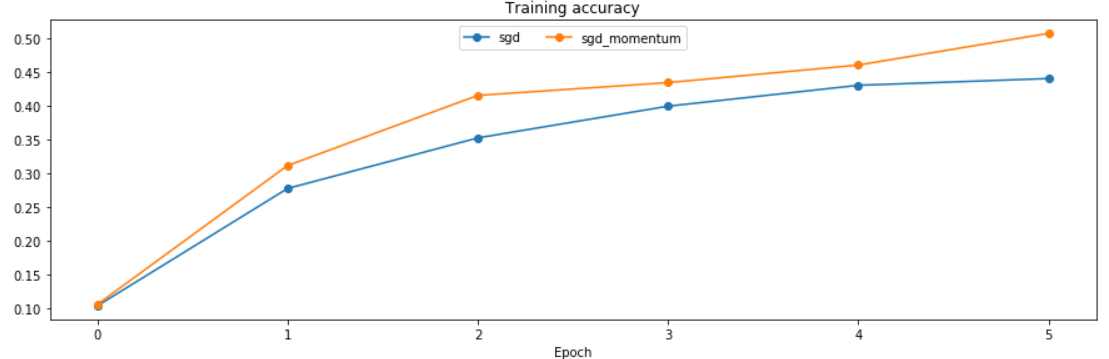
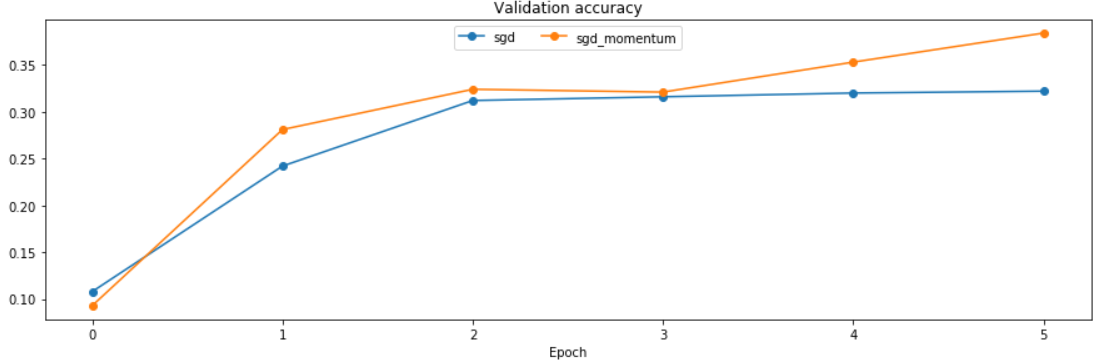
运行结果：
running with sgd
(Epoch 5 / 5) train acc: 0.440000; val_acc: 0.322000

running with sgd_momentum
(Epoch 5 / 5) train acc: 0.507000; val_acc: 0.384000



RMSProp and Adam

RMSprop关键代码

1
2
config['cache'] = config['decay_rate'] * config['cache'] +(1 - config['decay_rate']) * dw**2
next_w = w - config['learning_rate'] * dw / (np.sqrt(config['cache']) + config['epsilon'])

Adam算是RMSprop和动量的结合。
这里采用了偏差修正，所以要乘一个$\frac{1}{1-\beta^t}$，详情可参见笔记。
关键代码如下

1
2
3
4
5
6
config['t'] += 1
config['m'] = config['beta1'] * config['m'] + (1 - config['beta1']) * dw
config['v'] = config['beta2'] * config['v'] + (1 - config['beta2']) * (dw**2)
mb = config['m'] / (1 - config['beta1'] ** config['t'])
vb = config['v'] / (1 - config['beta2'] ** config['t'])
next_w = w - config['learning_rate'] * mb / (np.sqrt(vb) + config['epsilon'])

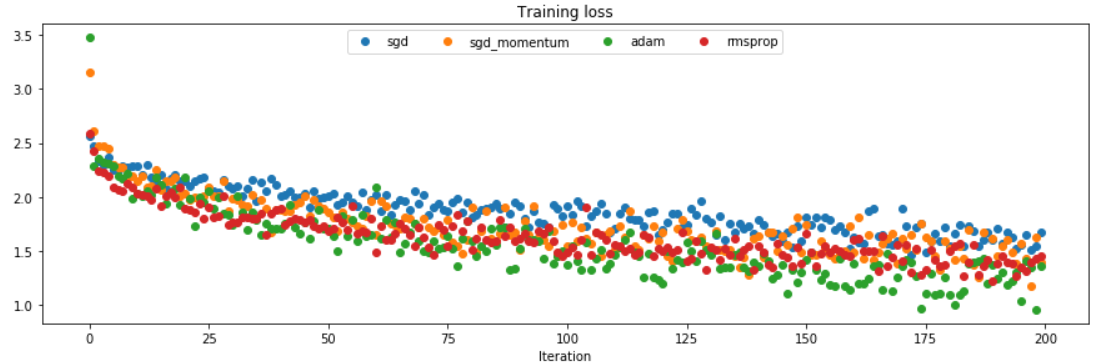
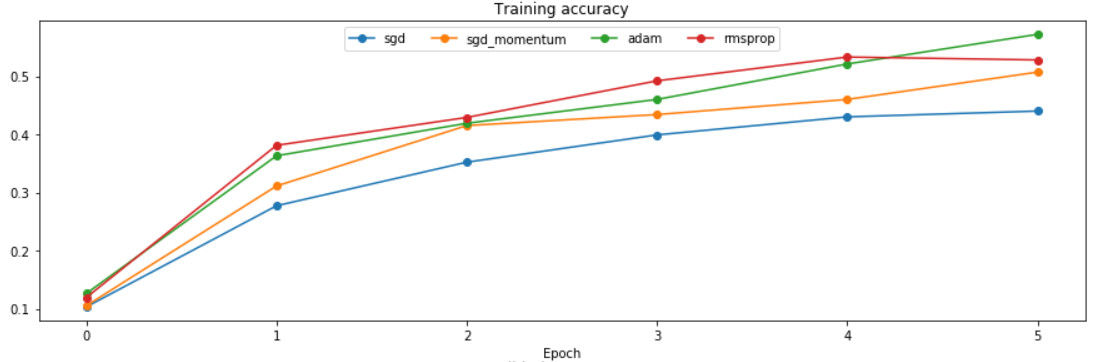
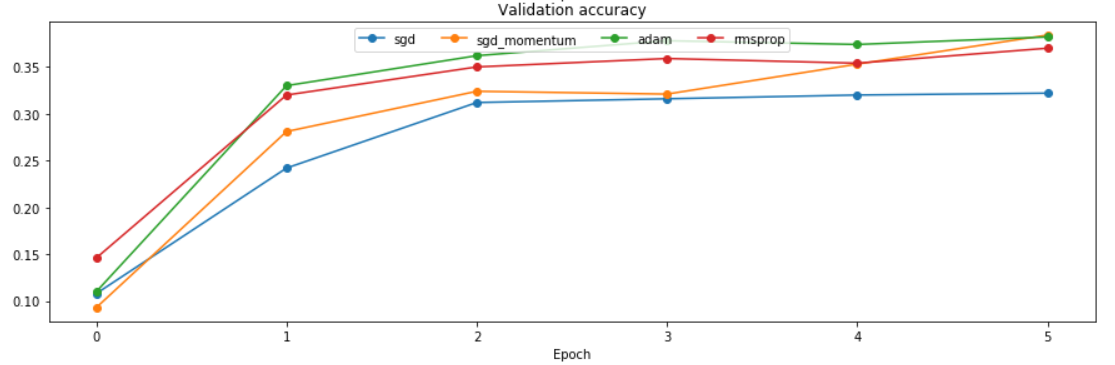
对比结果：



-------------The End-------------