cs231n assignment2(BatchNormalization)
参考论文:Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
论文笔记:Batch Normalization
在机器学习中,当机器学习方法的输入数据包含零均值和单位方差的不相关特征时,机器学习方法往往更有效。
Batch Normalization即将这个想法,应用到了每层网络的输入中。
BatchNorMalization实现
BN forward
归一化之后添加了两个scale and shift参数,使其压缩范围可以灵活变化。
公式如下,
注意:因为训练中计算均值和方差的时候,用的是batch来算的;测试时的mean和var使用训练时的指数加权平均数。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16if mode == 'train':
# cal the x_hat and y
x_mean = np.mean(x, axis=0)
x_var = np.var(x, axis=0)
x_hat = (x - x_mean) / np.sqrt(x_var + eps)
out = gamma * x_hat + beta
# cal the running_paras
running_mean = momentum * running_mean + (1 - momentum) * x_mean
running_var = momentum * running_var + (1 - momentum) * x_var
cache = (x, x_hat, x_mean, x_var, gamma, beta, eps)
elif mode == 'test':
x_hat = (x - running_mean) / np.sqrt(running_var + eps)
out = gamma * x_hat + beta
else:
raise ValueError('Invalid forward batchnorm mode "%s"' % mode)
BN backward
参考博文:传送门
对于每个batch,采用计算图求导的方法,进行求导。
计算图如下:
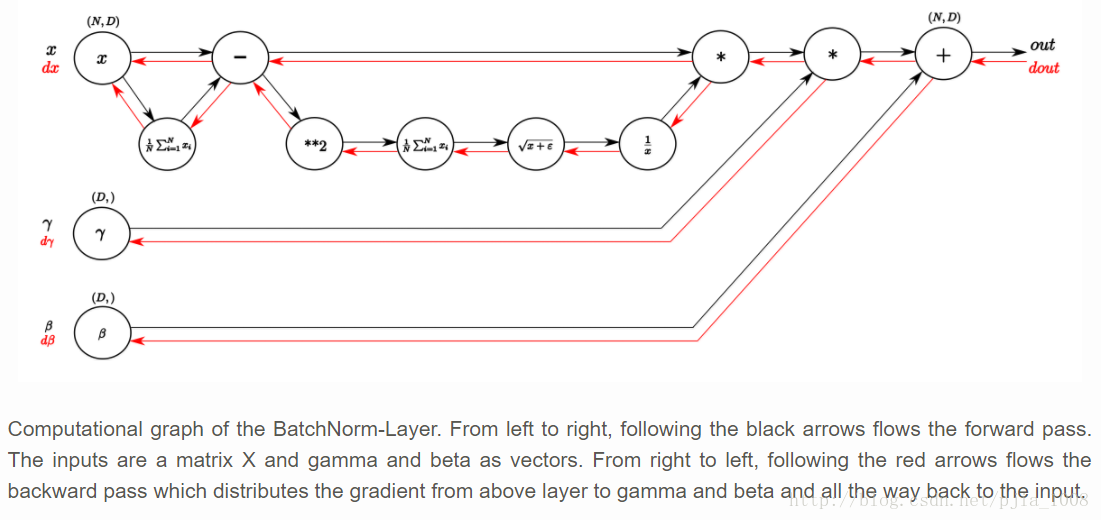
forward pass1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31N, D = x.shape
# step1: calculate mean
mu = 1./N * np.sum(x, axis=0)
# step2: subtract mean vector of every trainings example
xmu = x - mu
# step3: following the lower branch - calculation denominator
sq = xmu ** 2
# step4: calculate variance
var = 1./N * np.sum(sq, axis=0)
# step5: add eps for numerical stability, then sqrt
sqrtvar = np.sqrt(var + eps)
# step6: invert sqrtvar
ivar = 1./sqrtvar
# step7: execute normalization
xhat = xmu * ivar
# step8: Nor the two transformation steps
gammax = gamma * xhat
# step9
out = gammax + beta
# store intermediate
cache = (xhat, gamma, xmu, ivar, sqrtvar, var, eps)
backward pass1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39# unfold the variables stored in cache
xhat, gamma, xmu, ivar, sqrtvar, var, eps = cache
# get the dimensions of the input/output
N, D = dout.shape
# step9
dbeta = np.sum(dout, axis=0)
dgammax = dout # not necessary, but more understandable
# step8
dgamma = np.sum(dgammax * xhat, axis = 0)
dxhat = dgammax * gamma
# step7
divar = np.sum(dxhat * xmu, axis=0)
dxmu1 = dxhat * ivar
# step6
dsqrtvar = -1./(sqrtvar**2) * divar
# step5
dvar = 0.5 * 1./np.sqrt(var+eps) * dsqrtvar
# step4
dsq = 1./N * np.ones((N, D)) * dvar
# step3
dxmu2 = 2 * xmu * dsq
# step2
dx1 = (dxmu1 + dxmu2)
dmu = -1 * np.sum(dxmu1 + dxmu2, axis=0)
# step1
dx2 = 1./N * np.ones((N, D)) * dmu
# step0
dx = dx1 + dx2
BN alternative backward
将上文的梯度进行总和就得出了,链式求导的最终公式,论文也有给出。
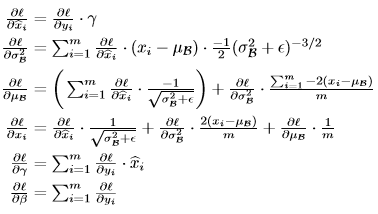
关键代码1
2
3
4
5
6
7
8
9
10x, x_hat, x_mean, x_var, gamma, beta, eps = cache
N, D = x.shape
dx_hat = dout * gamma
dx_var = -0.5 * np.sum(dx_hat * (x - x_mean) * np.power(x_var + eps, -3 / 2), axis=0)
dx_mean = np.sum(dx_hat * (-1. / np.sqrt(x_var + eps)), axis=0) + np.sum(-2 * dx_var * (x - x_mean), axis=0) / N
dx = dx_hat / np.sqrt(x_var + eps) + dx_var * 2 * (x - x_mean) / N + dx_mean / N
dgamma = np.sum(dout * x_hat, axis=0)
dbeta = np.sum(dout, axis=0)
Fully Connected Nets with BN
实现了BN模块,接着就在上节实验中的Fully Connected Nets类中加入BN层。
1 | # __init__ function |
Batch Normalization的实验结果
激活函数:ReLU
优化方法:Adam
with or without batch normalization
在5个隐层,每个隐层100个神经元的网络中,用1000个训练数据进行测试。分别用或者不用batch normalization1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21weight_scale = 2e-2
bn_model = FullyConnectedNet(hidden_dims, weight_scale=weight_scale, normalization='batchnorm')
model = FullyConnectedNet(hidden_dims, weight_scale=weight_scale, normalization=None)
bn_solver = Solver(bn_model, small_data,
num_epochs=10, batch_size=50,
update_rule='adam',
optim_config={
'learning_rate': 1e-3,
},
verbose=True,print_every=20)
bn_solver.train()
solver = Solver(model, small_data,
num_epochs=10, batch_size=50,
update_rule='adam',
optim_config={
'learning_rate': 1e-3,
},
verbose=True, print_every=20)
solver.train()
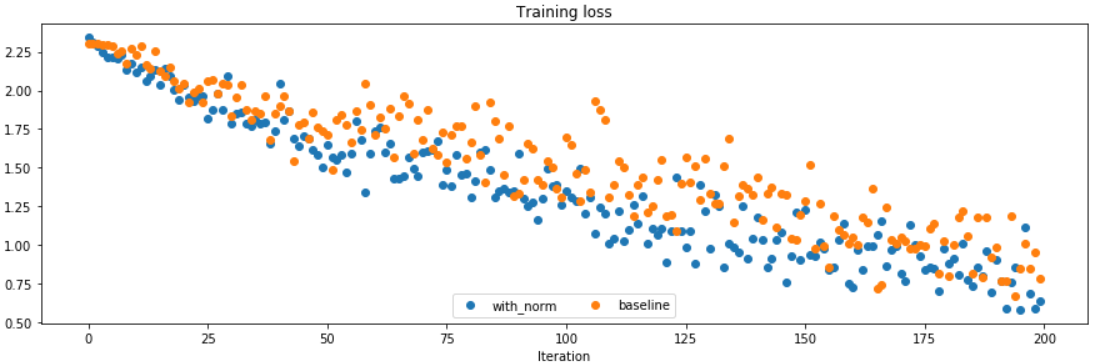
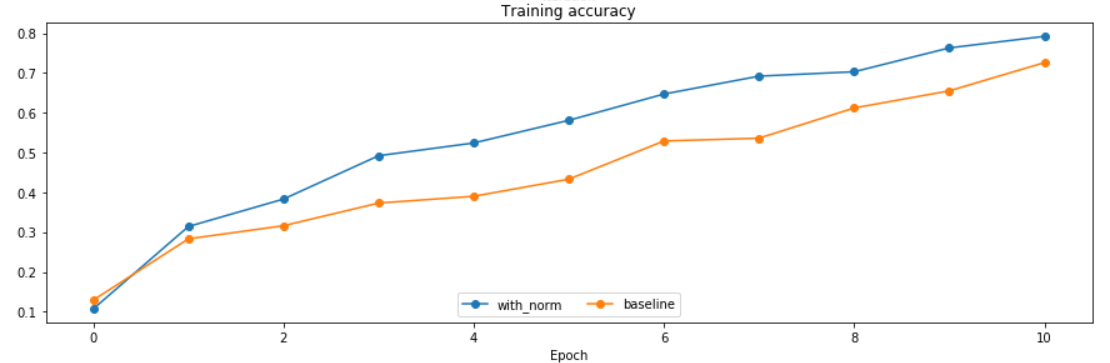
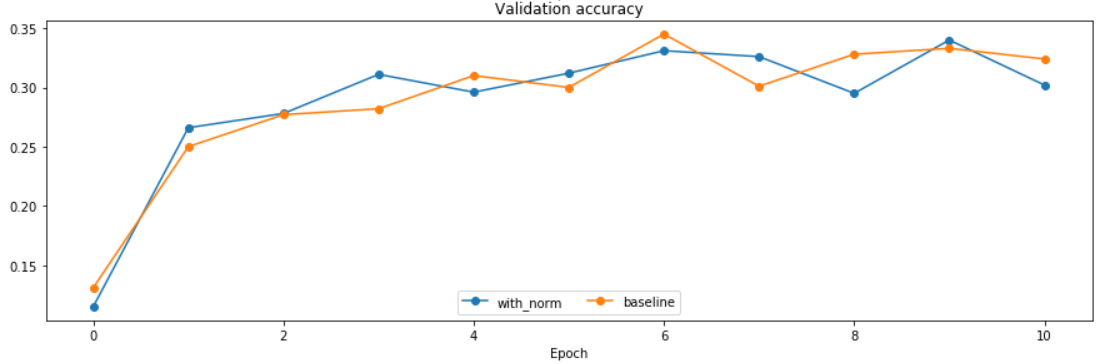
可以看到Adam优化,同样的学习率下,用batch normalization的网络loss下降更为快速,致使训练集拟合的更好。(两个泛化都很低)
different weight initialization scale
采用20种不同的weight initialization scale,查看with or without normalization的表现。


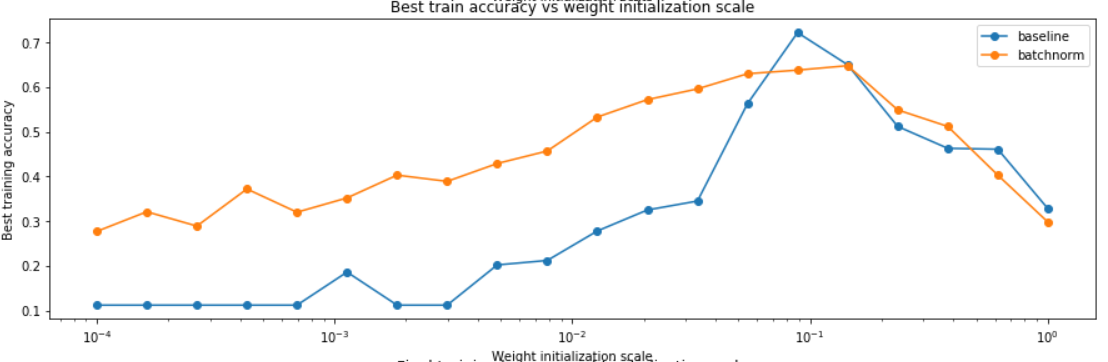
可以看出,在用较小的weight scale时,with norm的表现要更好。
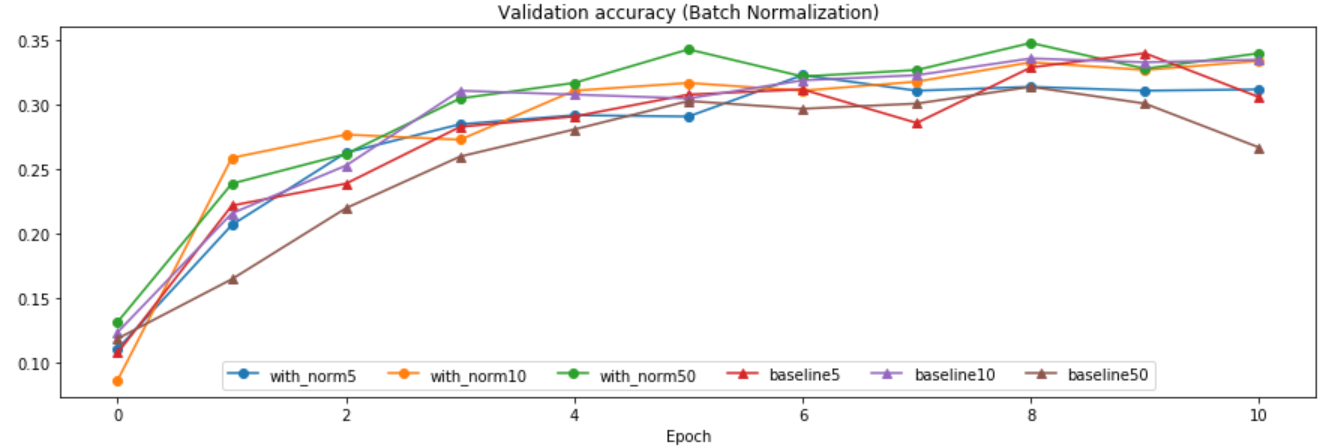
different batch size
因为Batch Normalization是对每个batch单独进行标准化,所以当batch size较小的时候,batch均值和方差不能很好的代表整体的均值和方差。
可以看到,当batch size到达一定值是,Batch Normalization才能显示出效果来。(同样,因为数据比较少,只观察拟合训练集的效果就好了)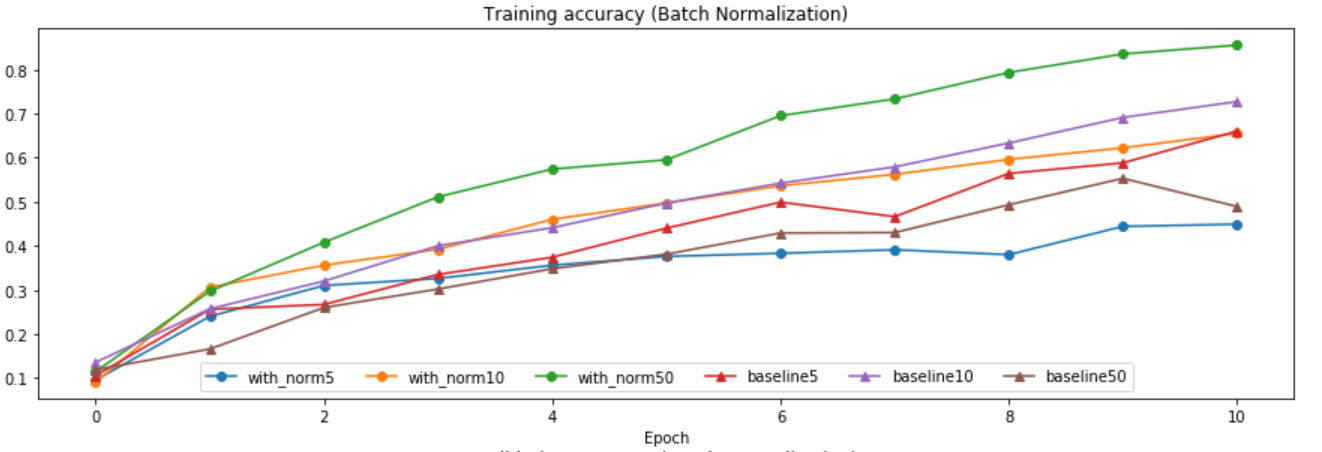
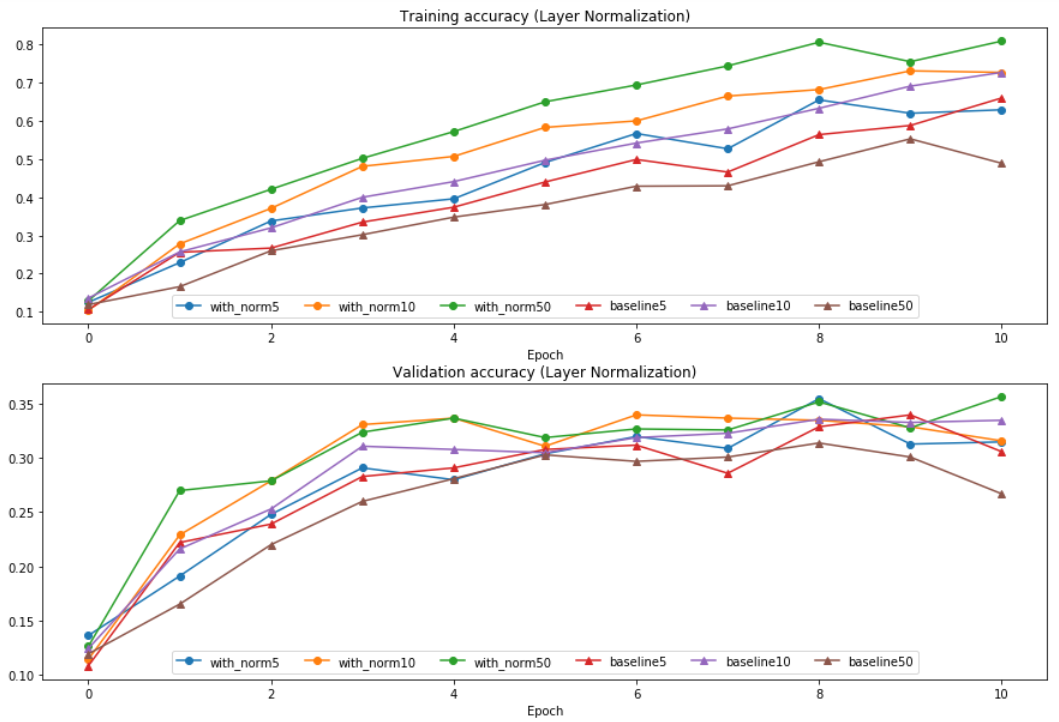
Layer Normalization
参见论文:Layer Normalization
原理
Batch Normalization是对输入数据在batch上做操作。比如输入为(N,D)的数据,求均值是对N个样本的各个维度分别求均值。所以需要较大的batch size。
而Layer Normalization是对输入的数据的每一个样本(1,D),求均值方差等等,不依赖batch。
Forward Pass
因为其原理与BN只是标准化的维度不同,代码只需在BN的基础上稍作修改。1
2
3
4
5
6
7
8
9
10# cal the x_hat and y
x_T = x.T
x_mean_T = np.mean(x_T, axis=0)
x_var_T = np.var(x_T, axis=0)
x_hat_T = (x_T - x_mean_T) / np.sqrt(x_var_T + eps)
x_hat = x_hat_T.T
out = gamma * x_hat + beta
cache = (x_T, x_hat_T, x_mean_T, x_var_T, gamma, beta, eps)
Backward Pass
同样,在BN的BP上稍作修改1
2
3
4
5
6
7
8
9
10
11
12
13
14
15x, x_hat, x_mean, x_var, gamma, beta, eps = cache
N, D = x.shape
dx_hat = dout * gamma
dx_hat_T = dx_hat.T
dx_var = -0.5 * np.sum(dx_hat_T * (x - x_mean) * np.power(x_var + eps, -3 / 2), axis=0)
dx_mean = np.sum(dx_hat_T * (-1 / np.sqrt(x_var + eps)), axis=0) + np.sum(-2 * dx_var * (x - x_mean), axis=0) / N
dx_T = dx_hat_T / np.sqrt(x_var + eps) + dx_var * 2 * (x - x_mean) / N + dx_mean / N
dx = dx_T.T
dgamma = np.sum(dout * x_hat.T, axis=0)
dbeta = np.sum(dout, axis=0)
return dx, dgamma, dbeta
实验结果
Layer Normalization因为不与batch size相关,可以看到其性能与batch size似乎关系不大。对比baseline有比较好的效果。