cs231n assignment2(Dropout)

Posted on | In | Visitors:
Words count in article: 1.5k | Reading time ≈ 5
Dropout；Add Random Noise；

cs231n assignment2(Dropout)

随机失活（Dropout）笔记

Dropout是一个简单又极其有效的正则化方法。该方法由Srivastava在论文Dropout: A Simple Way to Prevent Neural Networks from Overfitting中提出的，与L1正则化，L2正则化和最大范式约束等方法互为补充。在训练的时候，随机失活的实现方法是让神经元以超参数p的概率被激活或者被设置为0。

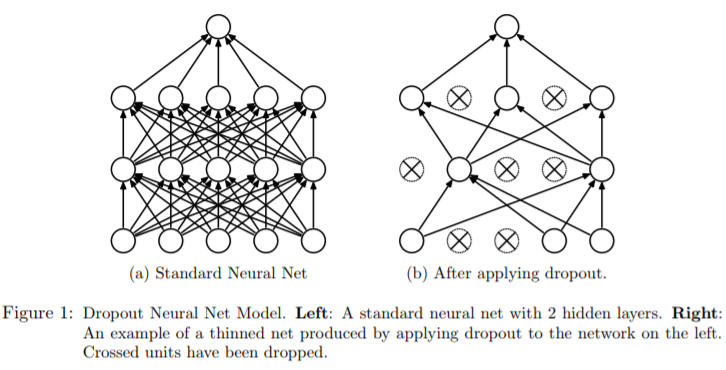
在训练过程中，随机失活可以被认为是对完整的神经网络抽样出一些子集，每次基于输入数据只更新子网络的参数（然而，数量巨大的子网络们并不是相互独立的，因为它们都共享参数）。在测试过程中不使用随机失活，可以理解为是对数量巨大的子网络们做了模型集成（model ensemble），以此来计算出一个平均的预测。

一个3层神经网络的普通版随机失活可以用下面代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
""" 普通版随机失活: 不推荐实现 (看下面笔记) """

p = 0.5 # 激活神经元的概率. p值更高 = 随机失活更弱

def train_step(X):
  """ X中是输入数据 """
  
  # 3层neural network的前向传播
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = np.random.rand(*H1.shape) < p # 第一个随机失活遮罩
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = np.random.rand(*H2.shape) < p # 第二个随机失活遮罩
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3
  
  # 反向传播:计算梯度... (略)
  # 进行参数更新... (略)

def predict(X):
  # 前向传播时模型集成
  H1 = np.maximum(0, np.dot(W1, X) + b1) * p # 注意：激活数据要乘以p
  H2 = np.maximum(0, np.dot(W2, H1) + b2) * p # 注意：激活数据要乘以p
  out = np.dot(W3, H2) + b3

注意：在predict函数中不进行随机失活，但是对于两个隐层的输出都要乘以p，调整其数值范围。这一点非常重要，因为在测试时所有的神经元都能看见它们的输入，因此我们想要神经元的输出与训练时的预期输出是一致的。以p=0.5为例，在测试时神经元必须把它们的输出减半，这是因为在训练的时候它们的输出只有一半。

上述操作不好的性质是必须在测试时对激活数据要按照p进行数值范围调整。既然测试性能如此关键，实际更倾向使用反向随机失活（inverted dropout），它是在训练时就进行数值范围调整，从而让前向传播在测试时保持不变。这样做还有一个好处，无论你决定是否使用随机失活，预测方法的代码可以保持不变。反向随机失活的代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
""" 
反向随机失活: 推荐实现方式.
在训练的时候drop和调整数值范围，测试时不做任何事.
"""

p = 0.5 # 激活神经元的概率. p值更高 = 随机失活更弱

def train_step(X):
  # 3层neural network的前向传播
  H1 = np.maximum(0, np.dot(W1, X) + b1)
  U1 = (np.random.rand(*H1.shape) < p) / p # 第一个随机失活遮罩. 注意/p!
  H1 *= U1 # drop!
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  U2 = (np.random.rand(*H2.shape) < p) / p # 第二个随机失活遮罩. 注意/p!
  H2 *= U2 # drop!
  out = np.dot(W3, H2) + b3

  # 反向传播:计算梯度... (略)
  # 进行参数更新... (略)

def predict(X):
  # 前向传播时模型集成
  H1 = np.maximum(0, np.dot(W1, X) + b1) # 不用数值范围调整了
  H2 = np.maximum(0, np.dot(W2, H1) + b2)
  out = np.dot(W3, H2) + b3**

Add Random Noise

Add Random Noise是一种常见的正则化思想。
在训练中，给网络添加一些随机性，在一定程度上扰乱它过拟合训练数据；
在测试中，要抵消掉所有的随机性，希望能够提高我们的泛化能力。
Dropout可能是最常见的使用这种策略的例子。

  • Dropout：随机失活（超参数p控制随机失活的力度）
  • Batch Normalization：训练中，一个样本可能与其他出现在不同的batch中，对于单个样本来说，如何正则化，具有一定随机性。（这种随机性不可控制力度）
  • Data Augmentation：在训练中，以某种方式随机的转换图像，使得标签可以不变，用转换过的图像进行训练。

水平翻转：
训练：反转后的图像
测试：原图像（？）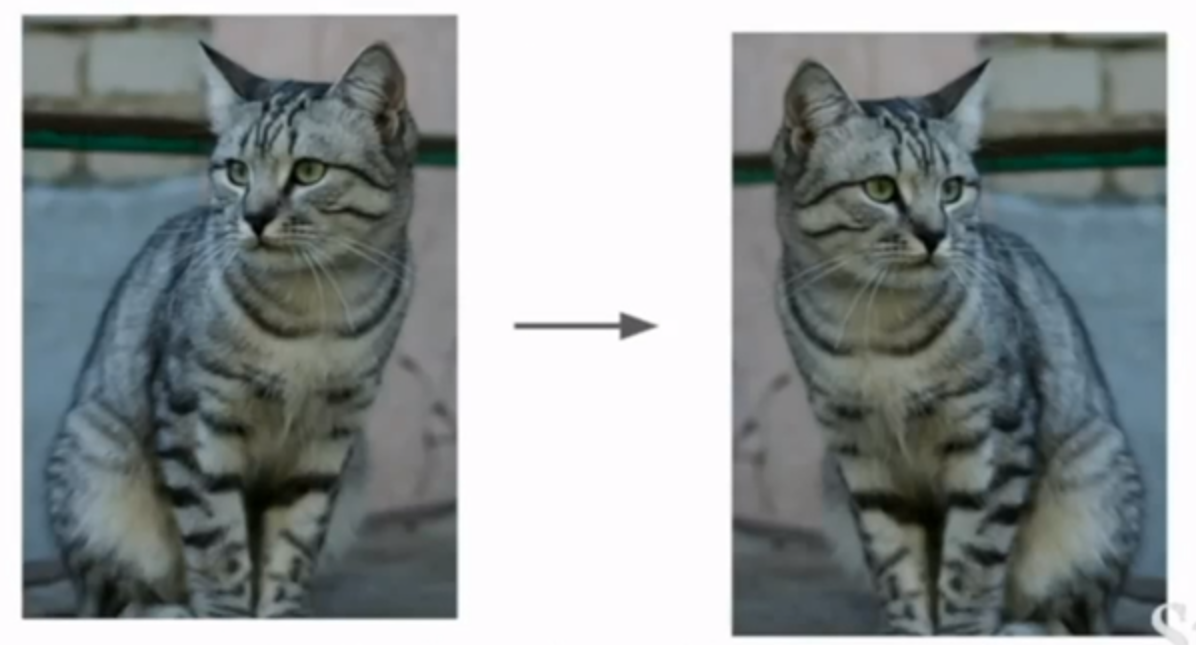

裁剪图像：
训练：从图像中随机抽取不同尺寸大小的裁剪图象。
测试：固定的裁剪图像

色彩抖动（Color Jitter）：
训练：随机改变图片的对比度和亮度或者其他更加复杂的色彩抖动的操作

More Complex:

  1. Apply PCA to all [R,G,B] pixels in training set
  2. Sample a “color offset” along priciple component directions
  3. Add offset to all pixels of a training image

  • DropConnect：随机将权重矩阵的一些值置零
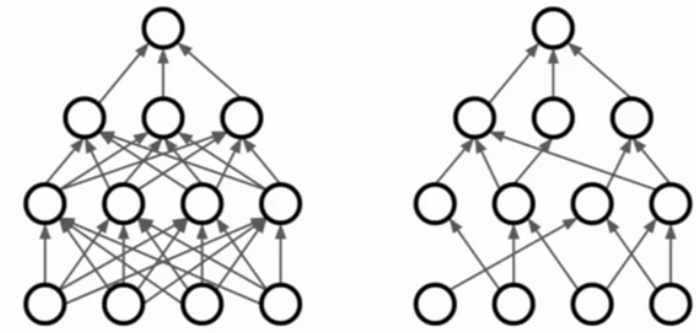
  • Fractional Max Pooling：训练时随机池化filters的大小，下图是可能的三种池化结果；测试时有很多方法抵消随机性。
  • Stochastic Depth：从网络中随机丢弃部分层；测试时用全部网络

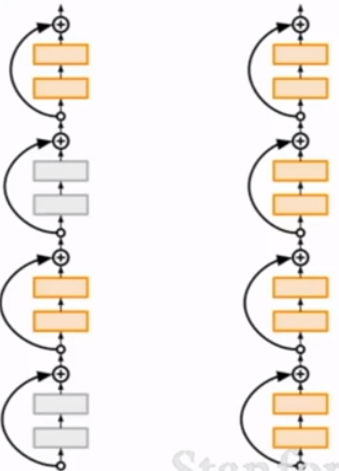
实验内容

roward pass

1
2
3
4
5
6
7
8
if mode == 'train':
    mask = (np.random.rand(*x.shape) < p) / p
    out = x * mask  # drop!
elif mode == 'test':
    out = x
    
cache = (dropout_param, mask)
out = out.astype(x.dtype, copy=False)

backward pass

1
2
3
4
5
6
7
dropout_param, mask = cache
mode = dropout_param['mode']

if mode == 'train':
    dx = dout * mask
elif mode == 'test':
    dx = dout

Fully-connected nets with Dropout

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# froward pass
for i in range(1, L):
    # ......
    # cal Z
    # cal A
    A, params['cache3'+str(i)] = relu_forward(Z)
    if self.use_dropout:
        A, params['cache4'+str(i)] = dropout_forward(A, self.dropout_param)
        
# backward pass
for i in range(L-1, 0, -1):
    # dropout
    if self.use_dropout:
        dA = dropout_backward(dA, params['cache4'+str(i)])
    # dA to dZ
    dZ = relu_backward(dA, params['cache3'+str(i)])
    # batchnorm
    # ......

训练结果

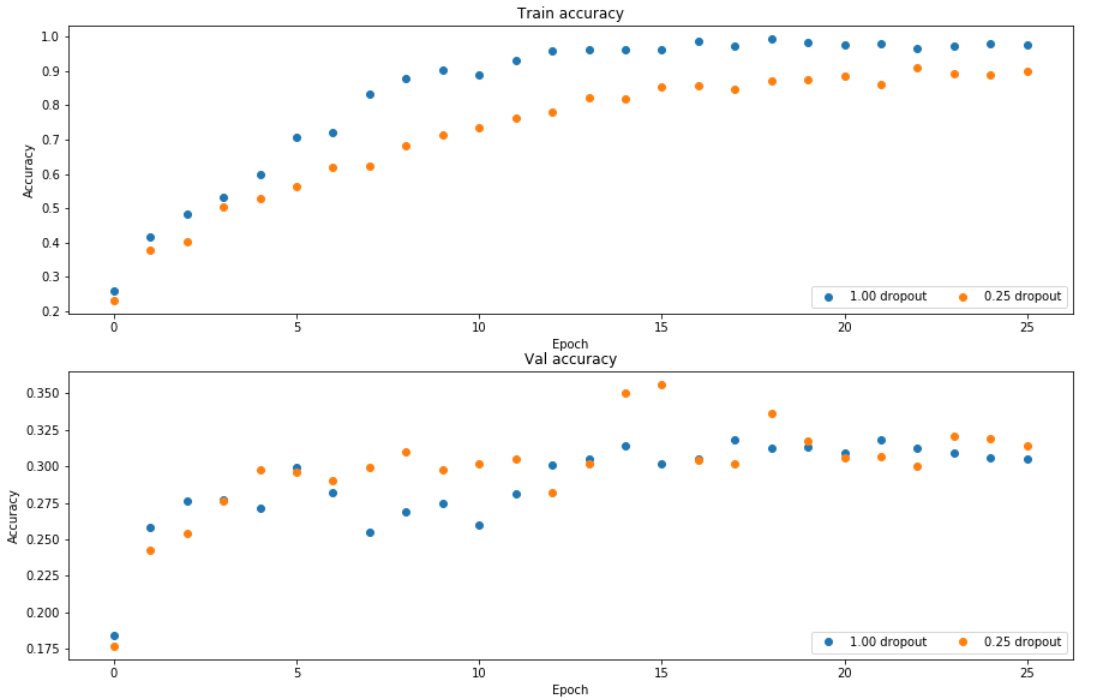
dropout（p=0.25）的网络，虽然训练收敛会变慢，但是在验证集中可以得出好的结果。

-------------The End-------------