cs231n assignment2(ConvolutionalNetworks)
Convolution: Naive forward pass
Input data of shape: $(N, C, H_{prev}, W_{prev})$
其中$N$是样本数,$C$是channel数。
下一层的$H,W$可由以下公式得出:
Output data of shape: $(N, F, H, W)$
其中$F$是本层filters的个数。
1 | def conv_forward_naive(x, w, b, conv_param): |
Convolution: Naive backward pass
在Forward Pass中,最关键的就这一句代码了
1 | Z[i, f, h_i, w_i] = np.sum(np.multiply(xi_slice, w[f])) + b[f] |
反向传播中,就根据这个来进行求导:
代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47def conv_backward_naive(dout, cache):
"""
A naive implementation of the backward pass for a convolutional layer.
Inputs:
- dout: Upstream derivatives.
- cache: A tuple of (x, w, b, conv_param) as in conv_forward_naive
Returns a tuple of:
- dx: Gradient with respect to x
- dw: Gradient with respect to w
- db: Gradient with respect to b
"""
###########################################################################
# TODO: Implement the convolutional backward pass. #
###########################################################################
x, w, b, conv_param = cache
stride = conv_param['stride'] # stride
pad = conv_param['pad'] # pad
N, C, H_prev, W_prev = x.shape
F, _, HH, WW = w.shape
N, F, H_out, W_out = dout.shape
# zero padding
x_pad = np.pad(x, ((0, 0), (0, 0), (pad, pad), (pad, pad)), 'constant', constant_values=0)
dx = np.zeros(x.shape)
dx_pad = np.zeros(x_pad.shape)
dw = np.zeros(w.shape)
db = np.zeros(b.shape)
for i in range(N): # loop over the batch of training examples
xi = x_pad[i] # Select ith training example's padded activation
for h_i in range(H_out): # loop over vertical axis of the output volume
for w_i in range(W_out): # loop over horizontal axis of the output volume
h_start = h_i * stride
h_end = h_start + HH
w_start = w_i * stride
w_end = w_start + WW
xi_slice = xi[:, h_start:h_end, w_start:w_end]
for f in range(F): # loop over channels (= #filters) of the output volume
dx_pad[i, :, h_start:h_end, w_start:w_end] += w[f] * dout[i, f, h_i, w_i]
dw[f] += xi_slice * dout[i, f, h_i, w_i]
db[f] += dout[i, f, h_i, w_i]
dx[i, :, :, :] = dx_pad[i,:, pad:-pad, pad:-pad]
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dw, db
Max-Pooling: Naive forward
Max-Pooling就对Convolution层简化一下就可以了。
Input data of shape: $(N, C, H_{prev}, W_{prev})$
其中$N$是样本数,$C$是channel数。
下一层的$H,W$:(没有考虑padding)
Output data of shape: $(N, C, H, W)$
1 | def max_pool_forward_naive(x, pool_param): |
Max-Pooling: Naive backward
对Max-Pooling的求导类似于max函数,最大为1,否则为0.1
2
3
4mask = (x == np.max(x))
##########等价于########
mask[i,j] = True if X[i,j] = x
mask[i,j] = False if X[i,j] != x
代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37def max_pool_backward_naive(dout, cache):
"""
A naive implementation of the backward pass for a max-pooling layer.
Inputs:
- dout: Upstream derivatives
- cache: A tuple of (x, pool_param) as in the forward pass.
Returns:
- dx: Gradient with respect to x
"""
###########################################################################
# TODO: Implement the max-pooling backward pass #
###########################################################################
x, pool_param = cache
pool_height = pool_param['pool_height']
pool_width = pool_param['pool_width']
stride = pool_param['stride'] # stride
N, C, H_out, W_out = dout.shape
dx = np.zeros(x.shape)
for i in range(N): # loop over the batch of training examples
for h_i in range(H_out): # loop over vertical axis of the output volume
for w_i in range(W_out): # loop over horizontal axis of the output volume
h_start = h_i * stride
h_end = h_start + pool_height
w_start = w_i * stride
w_end = w_start + pool_width
for c in range(C): # loop over channels (= #filters) of the output volume
x_slice = x[i, c, h_start:h_end, w_start:w_end]
mask = (x_slice == np.max(x_slice))
dx[i, c, h_start:h_end, w_start:w_end] += mask * dout[i, c, h_i, w_i]
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx
Spatial batch normalization: forward
由于维度的差别,卷积网络的Batch Normalization和全连接网络略有不同,卷积层的输入是$(N,C,H,W)$,BN是对每个batch的每个channel进行Normalization。及将每个channel看成全连接的一个属性:1
x_reshaped = x.transpose(0, 2, 3, 1).reshape(N * H * W, C)
x_reshaped就是新的$(N’,D’)$的输入。
代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37def spatial_batchnorm_forward(x, gamma, beta, bn_param):
"""
Computes the forward pass for spatial batch normalization.
Inputs:
- x: Input data of shape (N, C, H, W)
- gamma: Scale parameter, of shape (C,)
- beta: Shift parameter, of shape (C,)
- bn_param: Dictionary with the following keys:
- mode: 'train' or 'test'; required
- eps: Constant for numeric stability
- momentum: Constant for running mean / variance. momentum=0 means that
old information is discarded completely at every time step, while
momentum=1 means that new information is never incorporated. The
default of momentum=0.9 should work well in most situations.
- running_mean: Array of shape (D,) giving running mean of features
- running_var Array of shape (D,) giving running variance of features
Returns a tuple of:
- out: Output data, of shape (N, C, H, W)
- cache: Values needed for the backward pass
"""
out, cache = None, []
###########################################################################
# TODO: Implement the forward pass for spatial batch normalization. #
# #
# HINT: You can implement spatial batch normalization by calling the #
# vanilla version of batch normalization you implemented above. #
# Your implementation should be very short; ours is less than five lines. #
###########################################################################
N, C, H, W = x.shape
x_reshaped = x.transpose(0, 2, 3, 1).reshape(N * H * W, C)
out_tmp, cache = batchnorm_forward(x_reshaped, gamma, beta, bn_param)
out = out_tmp.reshape(N, H, W, C).transpose(0, 3, 1, 2)
return out, cache
Spatial batch normalization: backward
一样的思想应用于反向传播。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31def spatial_batchnorm_backward(dout, cache):
"""
Computes the backward pass for spatial batch normalization.
Inputs:
- dout: Upstream derivatives, of shape (N, C, H, W)
- cache: Values from the forward pass
Returns a tuple of:
- dx: Gradient with respect to inputs, of shape (N, C, H, W)
- dgamma: Gradient with respect to scale parameter, of shape (C,)
- dbeta: Gradient with respect to shift parameter, of shape (C,)
"""
dx, dgamma, dbeta = None, None, None
###########################################################################
# TODO: Implement the backward pass for spatial batch normalization. #
# #
# HINT: You can implement spatial batch normalization by calling the #
# vanilla version of batch normalization you implemented above. #
# Your implementation should be very short; ours is less than five lines. #
###########################################################################
N, C, H, W = dout.shape
dout_reshaped = dout.transpose(0, 2, 3, 1).reshape(N * H * W, C)
dx_reshaped, dgamma, dbeta = batchnorm_backward(dout_reshaped, cache)
dx = dx_reshaped.reshape(N, H, W, C).transpose(0, 3, 1, 2)
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dgamma, dbeta
Spatial group normalization: forward
Group Normalization是18年才提出来的一个方法,算是Layer Normalization的一种变形把,不同点是,将C个channels分成G个Group,对每个Group分别Normalizaiton。
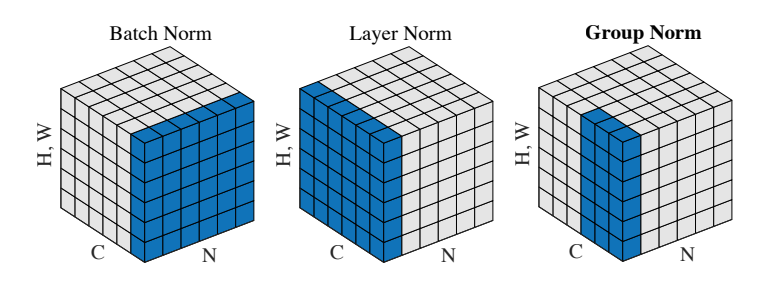
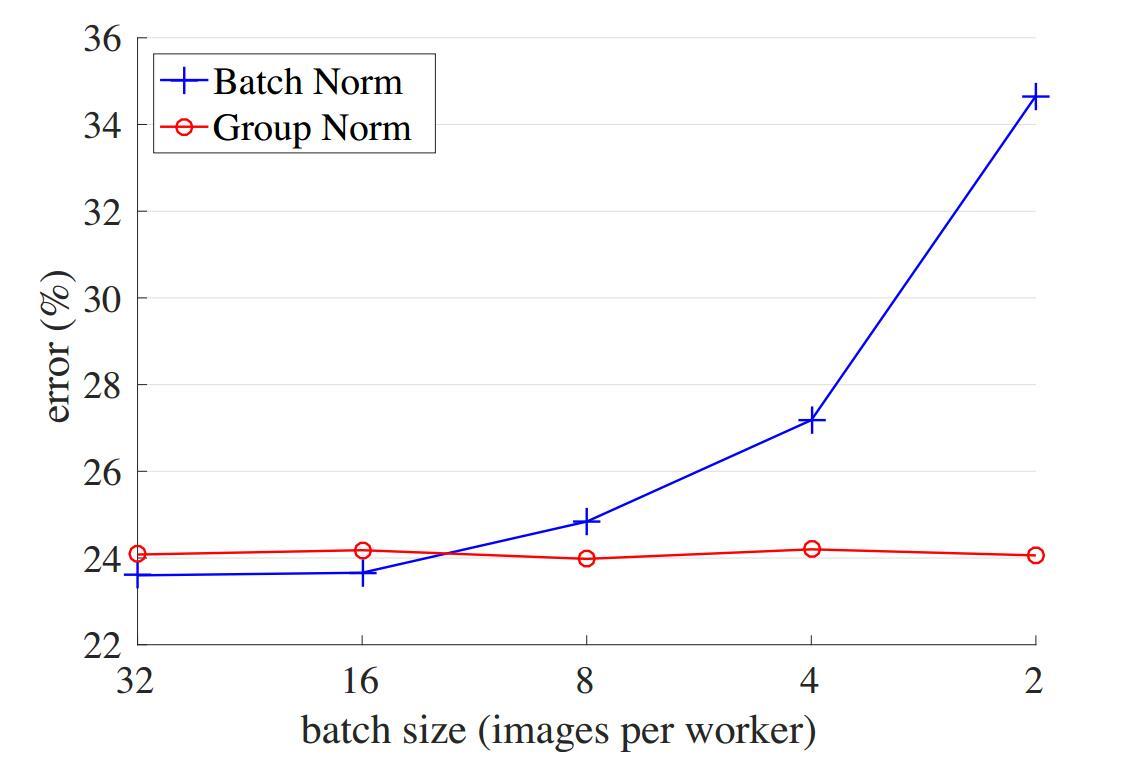
paper给的效果图,CNN中也一般,可能batch小一点的时候可以选用一下。
实现上,首先考类似上面那个BN的卷积版,每次要把一个batch$(N,C,H,W)$的哪些数据进行Normalization?
对于group normalization来说,1
2num = C // G
x_group = x.reshape(N*G, num*H*W)
就可以类似BN(或者LN)的应用了。
另外要注意,gamma和beta是,所以当涉及它们的运算的时候还要变成$(N, C,H,W)$
1 | def spatial_groupnorm_forward(x, gamma, beta, G, gn_param): |
Spatial group normalization: backward
反向传播稍微有点难??调的时候忽略了把LN代码中的N改为tmp_N = num * H * W。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
def spatial_groupnorm_backward(dout, cache):
"""
Computes the backward pass for spatial group normalization.
Inputs:
- dout: Upstream derivatives, of shape (N, C, H, W)
- cache: Values from the forward pass
Returns a tuple of:
- dx: Gradient with respect to inputs, of shape (N, C, H, W)
- dgamma: Gradient with respect to scale parameter, of shape (C,)
- dbeta: Gradient with respect to shift parameter, of shape (C,)
"""
###########################################################################
# TODO: Implement the backward pass for spatial group normalization. #
# This will be extremely similar to the layer norm implementation. #
###########################################################################
N, C, H, W = dout.shape
G, x, x_hat, x_mean, x_var, gamma, beta, eps = cache
num = C // G
# dx_hat (N, C, H, W)
dx_hat = dout * gamma
# Calculation with the shape of(N*G, num*H*W)
dx_hat = dx_hat.reshape(N*G, num*H*W)
dx_hat_T = dx_hat.T
tmp_N = num * H * W
dx_var = -0.5 * np.sum(dx_hat_T * (x - x_mean) * np.power(x_var + eps, -3 / 2), axis=0)
dx_mean = np.sum(dx_hat_T * (-1 / np.sqrt(x_var + eps)), axis=0) + np.sum(-2 * dx_var * (x - x_mean), axis=0) / tmp_N
dx_group_T = dx_hat_T / np.sqrt(x_var + eps) + dx_var * 2 * (x - x_mean) / tmp_N + dx_mean / tmp_N
dx = dx_group_T.T.reshape(N, C, H, W)
dgamma = np.sum(dout * x_hat, axis=(0,2,3)).reshape(1, C, 1, 1)
dbeta = np.sum(dout, axis=(0,2,3)).reshape(1, C, 1, 1)
###########################################################################
# END OF YOUR CODE #
###########################################################################
return dx, dgamma, dbeta