cs231n assignment3(LSTM_Captioning)

上个实验中的virtual RNN，存在一个问题，就是无法解决长期依赖问题（long-term dependencies）。当时间序列变得很长的时候，前后信息的关联度会越来越小，直至消失，即所谓的梯度消失现象。

GRU（Gated Recurrent Unit）单元

GRU用了个更新门的东西（它出现的时间比LSTM要晚），来维持一个长时间的记忆。

看一个例子：

The cat, which already ate …, was full.

这里我们看到，cat和was之间隔了一个很长的定语从句，在这之间RNN可能记不到之前的信息。

于是这里用一个c = memory cell来表示长期的记忆；一个更新门$f_u$来确定是否对c进行更新，因为可能并不是每次都对c进行改变，可以达到一个长期记忆的效果。

公式如下：

$$\tilde{c}^{<t>} = \tanh(W_c[c^{t-1}, x^{t}]+b_c)$$ $$f_u=\sigma(W_u[c^{t-1}, x^{t}]+b_u)$$ $$c^{<t>}=f_u*\tilde{c}^{t}+(1-f_u)*c^{t-1}$$

Sigma函数使$f_u$很容易就非常接近1或0。

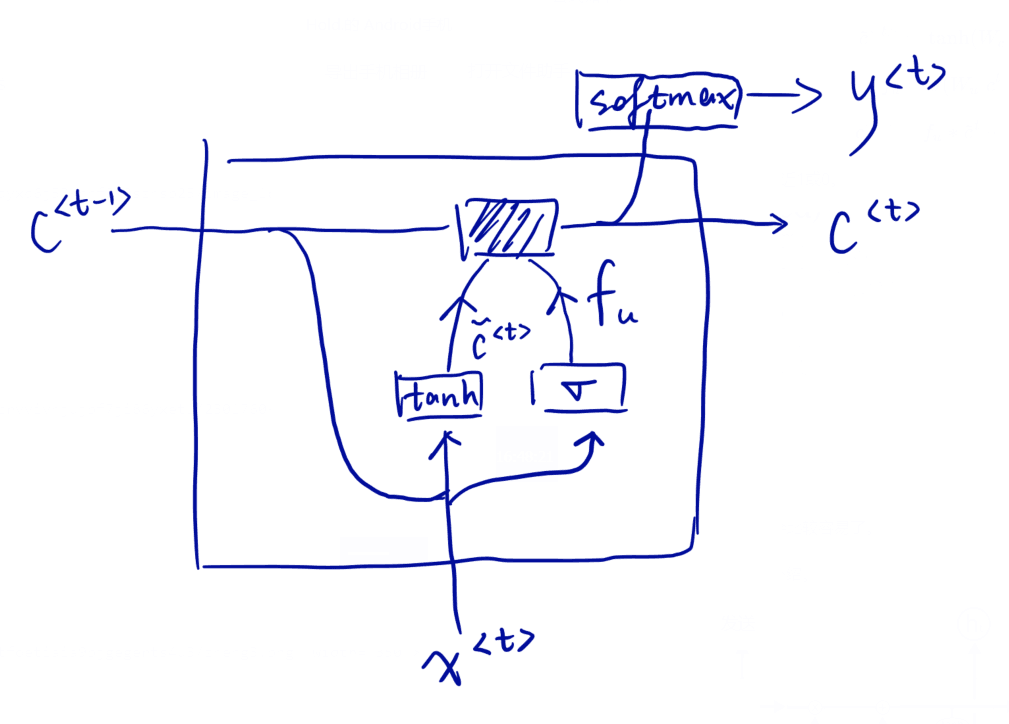
LSTM原理

有了门的概念之后，理解LSTM会比较容易了。

一个LSTM单元有三个门，后面介绍。

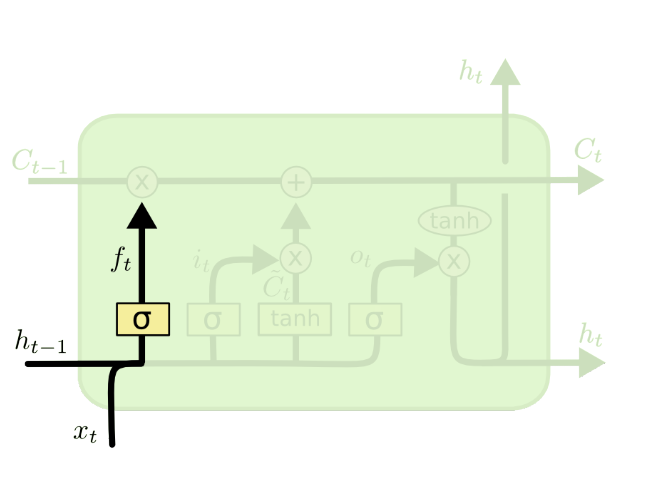
遗忘门

遗忘门决定对上次的$c^{}$“遗忘程度”。

$$f_t=\sigma(W_t[c^{<t-1>}, x^{<t>}]+b_t)$$

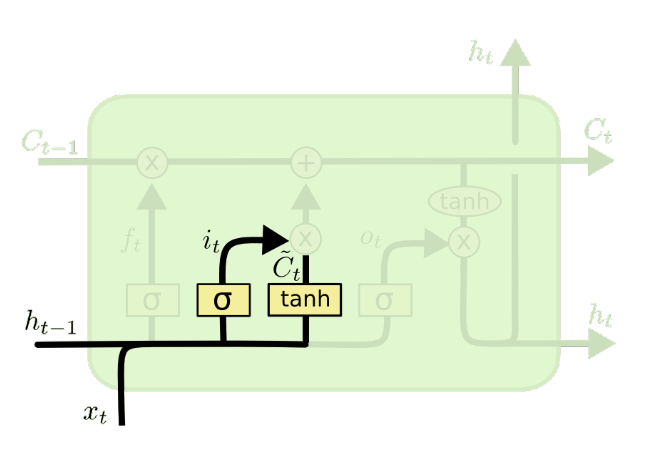
更新门

更新门决定对本次计算新生成的$\tilde{c}^{}$“保留程度”

$$f_i=\sigma(W_i[c^{<t-1>}, x^{<t>}]+b_i)$$

同时计算一下memory cell的值

$$\tilde{c}^{<t>} = \tanh(W_c[c^{<t-1>}, x^{<t>}]+b_c)$$

有了更新门和遗忘门还有新的memory cell，就可以对memory cell进行更新

$$c^{<t>}=f_t*c^{<t-1>}+f_i*\tilde{c}^{<t>}$$

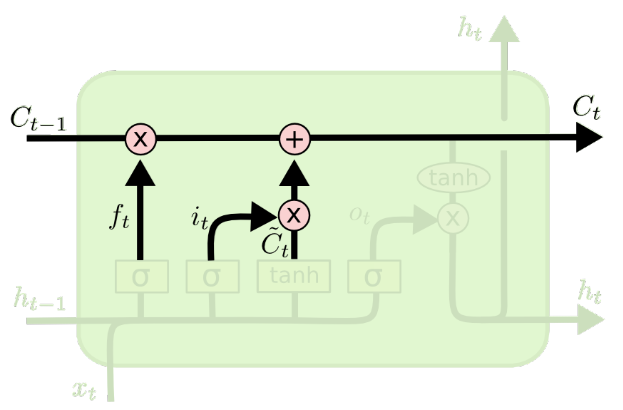
输出门

更新门和遗忘门都是针对$c^{}$的更新而言的，输出门则是针对$f^{}$来说的。

$$o_t=\sigma(W_o[c^{<t-1>}, x^{<t>}]+b_o)$$ $$h^{<t>} = o_t * \tanh(c^{<t>})$$

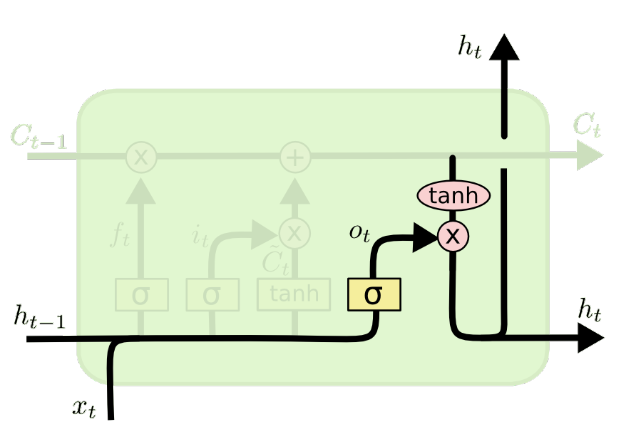
以上就是标准的LSTM，当然它还有很多变体这里就不再介绍。下面是作业内容。

LSTM Step

Forward Pass

def lstm_step_forward(x, prev_h, prev_c, Wx, Wh, b):
    """
    Inputs:
    - x: Input data, of shape (N, D)
    - prev_h: Previous hidden state, of shape (N, H)
    - prev_c: previous cell state, of shape (N, H)
    - Wx: Input-to-hidden weights, of shape (D, 4H)
    - Wh: Hidden-to-hidden weights, of shape (H, 4H)
    - b: Biases, of shape (4H,)

    Returns a tuple of:
    - next_h: Next hidden state, of shape (N, H)
    - next_c: Next cell state, of shape (N, H)
    - cache: Tuple of values needed for backward pass.
    """
    N, D = x.shape
    A = np.dot(x, Wx) + np.dot(prev_h, Wh) + b
    A = A.reshape(N, 4, -1)
    next_c = sigmoid(A[:,1,:]) * prev_c + sigmoid(A[:,0,:]) * np.tanh(A[:,3,:])
    next_h = sigmoid(A[:,2,:]) * np.tanh(next_c)

    cache = (A, x, prev_h, prev_c, Wx, Wh, b, next_h, next_c)

    return next_h, next_c, cache

Backward Pass

不用推公式，用计算图递归求导就好了。

def lstm_step_backward(dnext_h, dnext_c, cache):
    """
    Backward pass for a single timestep of an LSTM.

    Inputs:
    - dnext_h: Gradients of next hidden state, of shape (N, H)
    - dnext_c: Gradients of next cell state, of shape (N, H)
    - cache: Values from the forward pass

    Returns a tuple of:
    - dx: Gradient of input data, of shape (N, D)
    - dprev_h: Gradient of previous hidden state, of shape (N, H)
    - dprev_c: Gradient of previous cell state, of shape (N, H)
    - dWx: Gradient of input-to-hidden weights, of shape (D, 4H)
    - dWh: Gradient of hidden-to-hidden weights, of shape (H, 4H)
    - db: Gradient of biases, of shape (4H,)
    """
    A, x, prev_h, prev_c, Wx, Wh, b, next_h, next_c = cache

    dsigmoid_a2 = dnext_h * np.tanh(next_c)
    dnext_c += dnext_h * sigmoid(A[:, 2, :]) * (1 - np.tanh(next_c) ** 2)
    dsigmoid_a1 = dnext_c * prev_c
    dsigmoid_a0 = dnext_c * np.tanh(A[:, 3, :])
    dtanh_a3 = dnext_c * sigmoid(A[:, 0, :])
    dA = np.zeros(A.shape)
    dA[:, 0, :] = dsigmoid_a0 * sigmoid(A[:, 0, :]) * (1 - sigmoid(A[:, 0, :]))
    dA[:, 1, :] = dsigmoid_a1 * sigmoid(A[:, 1, :]) * (1 - sigmoid(A[:, 1, :]))
    dA[:, 2, :] = dsigmoid_a2 * sigmoid(A[:, 2, :]) * (1 - sigmoid(A[:, 2, :]))
    dA[:, 3, :] = dtanh_a3 * (1 - np.tanh(A[:, 3, :]) ** 2)

    dprev_c = dnext_c * sigmoid(A[:, 1, :])
    N, D = x.shape
    dA = dA.reshape(N, -1)

    dx = dA.dot(Wx.T)
    dWx = x.T.dot(dA)
    dprev_h = dA.dot(Wh.T)
    dWh = prev_h.T.dot(dA)
    db = np.ones((N,)).dot(dA)
    
    return dx, dprev_h, dprev_c, dWx, dWh, db

LSTM

这一部分与RNN差不多。

Forward Pass

def lstm_forward(x, h0, Wx, Wh, b):
    """
    Forward pass for an LSTM over an entire sequence of data.

    Inputs:
    - x: Input data of shape (N, T, D)
    - h0: Initial hidden state of shape (N, H)
    - Wx: Weights for input-to-hidden connections, of shape (D, 4H)
    - Wh: Weights for hidden-to-hidden connections, of shape (H, 4H)
    - b: Biases of shape (4H,)

    Returns a tuple of:
    - h: Hidden states for all timesteps of all sequences, of shape (N, T, H)
    - cache: Values needed for the backward pass.
    """
    N, T, D = x.shape
    H = h0.shape[1]
    cache = []
    h = np.zeros((N, T, H))
    prev_h = h0
    prev_c = np.zeros((N, H))
    for t in range(T):
        prev_h, prev_c, cache_t = lstm_step_forward(x[:, t, :], prev_h, prev_c, Wx, Wh, b)
        cache.append(cache_t)
        h[:, t, :] = prev_h

    return h, cache

Backward Pass

def lstm_backward(dh, cache):
    """
    Backward pass for an LSTM over an entire sequence of data.]

    Inputs:
    - dh: Upstream gradients of hidden states, of shape (N, T, H)
    - cache: Values from the forward pass

    Returns a tuple of:
    - dx: Gradient of input data of shape (N, T, D)
    - dh0: Gradient of initial hidden state of shape (N, H)
    - dWx: Gradient of input-to-hidden weight matrix of shape (D, 4H)
    - dWh: Gradient of hidden-to-hidden weight matrix of shape (H, 4H)
    - db: Gradient of biases, of shape (4H,)
    """
    _, x, prev_h, prev_c, Wx, Wh, b, next_h, next_c = cache[0]
    N, T, H = dh.shape
    D = x.shape[1]
    dx = np.zeros((N, T, D))
    dh0 = np.zeros((N, H))
    dWx = np.zeros((D, 4 * H))
    dWh = np.zeros((H, 4 * H))
    db = np.zeros((4*H))
    dprev_c = np.zeros((N, H))
    for t in range(T-1, -1, -1):
        dx_t, dh0, dprev_c, dWx_t, dWh_t, db_t = lstm_step_backward(dh[:, t, :] + dh0, dprev_c, cache[t])
        dx[:,t,:] = dx_t
        dWx += dWx_t
        dWh += dWh_t
        db += db_t
    return dx, dh0, dWx, dWh, db

loss,grads,sample稍微修改一点就好。