西瓜书笔记7 贝叶斯分类器

先验概率：事情还没有发生，要求这件事情发生的可能性的大小

后验概率：事情已经发生，要求这件事情发生的原因是由某个因素引起的可能性的大小

贝叶斯定理:

$P(A|B) = \frac{P(AB)}{P(B)}=\frac{P(B|A)P(A)}{P(B)}$

贝叶斯决策论

假设有$N$个可能的类别标记，即 $\gamma=\lbrace{c}_{1},{c}_{2},…,{c}_{N}\rbrace$

${\lambda}_{ij}$是将一个真实标记为${c}_{j}$样本误分类为${c}_{i}$的概率。

将样本$\boldsymbol x$分类为${c}_{i}$产生的期望损失为

$R({C}_{i}|\boldsymbol{x})=\sum_{j=1}^{N} {\lambda}_{ij}P(c_{i}|\boldsymbol{x})$

后验概率$P({c}_{j}|\boldsymbol{x})$理解：$\boldsymbol{x}$已经存在的情况下，$c_{j}$发生的概率，即$\boldsymbol{x}$分类为$c_{j}$的概率

我们的任务是寻找一个判定准则$h:\chi \rightarrow \gamma$以最小化总体风险

$R(h)=E_{\boldsymbol{x}}[R(h(\boldsymbol{x})|\boldsymbol{x})]$

贝叶斯判定准则：为最小化总体风险，只需在每个样本上选择那个能使条件风险$R(c|\boldsymbol{x})$最小的标记，即

$h^{*}(\boldsymbol{x})=\underset{c\epsilon{\gamma}}{argmin}R(c|\boldsymbol{x})$

若目标是最小化分类错误率，可采用0/1损失函数，则误判损失${\lambda}_{ij}$可写为

$\lambda_{ij} = \left\{\begin{matrix} 0,&if\ i=j; \\ 1,&otherwise \end{matrix}\right.$

此时条件风险

$R(c|\boldsymbol{x})=1-P(c|\boldsymbol{x})$

目标最小化风险$R(c|\boldsymbol{x})$，即最大化$P(c|\boldsymbol{x})$
于是最小化分类错误率的贝叶斯最有分类器为

$h^{*}(\boldsymbol{x})=\underset{c\epsilon{\gamma}}{argmax}P(c|\boldsymbol{x})$

大体来说，有两种测率来估计后验概率$P(c|\boldsymbol{x})$：

判别式模型：给定$\boldsymbol{x}$，可通过直接建模$P(c|\boldsymbol{x})$来预测c。

生成式模型：先对联合概率分布$P(c, \boldsymbol{x})$建模，然后在由此获得$P(c|\boldsymbol{x})$。

常见判别式模型：

线性回归、逻辑回归

线性判别分析

支持向量机(SVM)

神经网络(Neural Networks)

随机森林、决策树

Boosting

常见生成式模型:

隐马尔科夫模型(HMM)

朴素贝叶斯模型

高斯混合模型(GMM)

AODE(SPODE的集成)

Latent Dirichlet allocation

Restricted Boltzmann Machine

对于生成式模型来说，必然考虑

$P(c|\boldsymbol{x})=\frac{P(c,\boldsymbol{x})}{P(\boldsymbol{x})}$

根据贝叶斯定理

$P(c|\boldsymbol{x})=\frac{P(c)P(\boldsymbol{x}|c)}{P(\boldsymbol{x})}$

$P(c)$是类“先验”概率。表达了样本空间中各类样本所占的比例，根据大数定律，当训练集包含充足的独立同分布样本时，P(c)可通过各类样本出现的频率来估计。

$P(\boldsymbol{x})$是用于归一化的“证据”因子，对所有类标记均相同。个人认为是$\boldsymbol{x}$在所有样本空间里出现的概率。

$P(\boldsymbol{x}|c)$是样本$\boldsymbol{x}$相对于标记c的类条件概率，或称为“似然”，标记为c的样本中标记为$\boldsymbol{x}$的概率。

$P(\boldsymbol{x}|c)$怎么估计？

不可用频率估计

由于$P(\boldsymbol{x}|c)$涉及关于$\boldsymbol{x}$的所有属性的联合概率。假设样本有d个属性，每个属性都是二值，则样本空间将有$2^{d}$种可能的取值。现实应用中这个值往往大于样本数，也就是说，很多样本取值在训练集中根本没有出现。直接用频率估计$P(\boldsymbol{x}|c)$显然是不同的，因为“未被观测到”和“出现概率为零”通常是不同的。

极大似然估计：先假设其具有某种确定的概率分布形式，再基于训练样本对参数进行估计。

假设$P(\boldsymbol{x}|c)$具有确定的形式并且被参数向量$\boldsymbol{\theta_{c}}$唯一确定

我们的任务就是用训练集D估计参数$\boldsymbol{\theta_{c}}$。为明确起见，可将$P(\boldsymbol{x}|c)$记为$P(\boldsymbol{x}|\boldsymbol{\theta_{c}})$。

令$D_{c}$表示训练集D中第c类样本组成的集合，假设这些样本是独立同分布的，则参数$\boldsymbol{\theta_{c}}$对于$D_{c}$的似然是
$P(D_{c}|\boldsymbol{\theta_{c}}) = \prod_{\boldsymbol{x}\epsilon{D_{c}}}P(\boldsymbol{x}|\boldsymbol{\theta_{c}})$
避免练成操作造成的下溢，通常使用对数似然
$LL(\boldsymbol{\theta_{c}}) = logP(D_{c}|\boldsymbol{\theta_{c}}) =\sum_{\boldsymbol{x}\epsilon{D_{c}}}logP(\boldsymbol{x}|\boldsymbol{\theta_{c}})$
参数$\boldsymbol{\theta_{c}}$的极大似然估计$\hat{\boldsymbol{\theta}}_{c}$为
$\hat{\boldsymbol{\theta}}_{c}=\underset{\boldsymbol{\theta_{c}}}{argmax}LL(\boldsymbol{\theta_{c}})$
需要注意的是，这种参数化的方法虽然能使类条件概率估计变得相对简单，但估计结果的准确性严重依赖于所假设的概率分布形式是否符合潜在的真是数据分布。

朴素贝叶斯分类器

属性条件独立假设

属性条件独立性假设：对已知类别，假设所有属性相互独立。

基于属性条件独立性假设：

$P(c|\boldsymbol{x})=\frac{P(c)P(\boldsymbol{x}|c)}{P(\boldsymbol{x})}=\frac{P(c)}{P({\boldsymbol{x}})}\prod_{i=1}^{d}P(x_{i}|c)$

其中$d$为属性数目，$x_{i}$为$\boldsymbol{x}$在第$i$个属性上的取值。

对所有类别来说$P(\boldsymbol{x})$相同，所以朴素贝叶斯的表达式为：

$h_{nb}(\boldsymbol{x}) = \underset{c\epsilon{\gamma}}{argmax}P(c)\prod_{i=1}^{d}P(x_{i}|c)$

令$D_{c}$表示训练集$D$中第$c$类样本组成的集合，若有重组的独立同分布样本，则可容易地估计出类先验概率

$P(c) = \frac{|D_{c}|}{|D|}$

对离散属性而言，令$D_{c,x_{i}}$表示$D_{c}$中在第i个属性上取值为$x_{i}$的样本组成的集合，条件概率$P(x_{i}|c)$可估计为

$p(x_{i}|c)=\frac{|D_{c,x_{i}}|}{|D_{c}|}$

对连续属性而言，可考虑概率密度函数。假定$p(x_{i}|C)\sim N(\mu_{c,i},\sigma_{c,i}^{2})$，其中$\mu_{c,i}$和$\sigma_{c,i}^{2}$分别是第c类样本在第i个属性上取值的均值和方差(易求)，则有

$p(x_i|c)=\frac{1}{\sqrt{2\pi}\sigma_{c,i}}exp(-\frac{(x_i-\mu_{c,i})^2}{2 \sigma_{c,i}^2})$

拉普拉斯修正

需注意，若某个属性值在训练集中没有与某个类同时出现过，则直接基于上式进行估计，则会出现问题。例如，

$p(x_{i}|c)=\frac{|D_{c,x_{i}}|}{|D_{c}|} = \frac{0}{D_c} = 0$

则其与其他属性的乘积都为0。为了避免其他属性携带的信息被训练集中未出现的属性值“抹去”，在估计概率值是通常需要“平滑”，常用“拉普拉斯修正”。

令$N$表示训练集$D$中可能的属性数，$N_i$表示第$i$个属性可能的取值数，则

$\hat{P}(c)=\frac{|D_c|+1}{|D|+N}$ $\hat{P}(x_i|c)=\frac{|D_{c,xi}|+1}{|D_c|+N}$

拉普拉斯修正实质上假设了属性值与类别均匀分布。

现实任务中朴素贝叶斯分类器有多种使用方式。例如：

若任务队预测速度要求较高，可对所有概率估值事件预处理储存，预测时“查表”

若任务数据更替频繁，可采用“懒惰学习”

若数据不断增加，可实现“增量学习”

半朴素贝叶斯分类器

思想：适当考虑一部分属性间的相互依赖信息，从而既不需要进行完全联合概率计算，又不至于彻底忽略了较强的属性依赖关系。

独立依赖估计

“独依赖估计”(One-Dependent Estimator)是最常用的一种策略：假设每个属性在类别之外最多仅依赖于一个其他属性，即

$P(c|\boldsymbol{x})\propto P(c)\prod_{i}^{d}P(x_i|c,pa_{i})$

其中$\propto$表示成正比，$pa_i$为属性$x_i$所依赖的属性，为$x_i$的父属性。

所以，问题的关键在如何确定每个属性的父属性。

SPODE

最直接的做法是，假设所有属性都依赖于同一个属性，称为“超父”。然后通过交叉验证等模型选择方法来确定超父属性，由此形成了SPODE(Super-Parent ODE)方法。

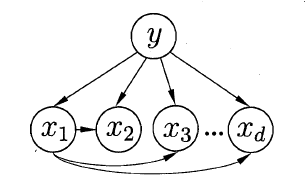
TAN

基于最大权生成树算法：

计算任意两个属性之间的条件互信息
$I(x_i, x_j|y)=\sum_{x_i,x_j;c\epsilon \gamma}log\frac{P(x_i,x_j|c)}{P(x_i|c)P(x_j|c)} ;$
以属性为结点构建完全图，任意两个结点之间边的权重设为 $I(x_i,x_j|y)$;
构建此完全图的最大权生成树，挑选跟变量，将边置为有向；
加入类别结点，增加y到每个属性的有向边。

条件互信息$I(x_i,x_j|y)$刻画了属性$x_i$和$x_j$在已知类别情况下的相关性，因此，通过最大生成树算法，TAN仅保留了强相关属性之间的依赖性

AODE

AODE(Averaged ODE)尝试将每个属性作为超父来构建SPODE，将具有足够数据支撑的SPODE集成起来作为最终结果，

$P(c|\boldsymbol x)\propto \sum_{i=1,|D_{x_i}| \geq m^{'}}^{d}P(c,x_i)\prod_{j=1}^{d}P(x_j|c,x_i)$

其中$D_{x_i}$是在第i个属性上取值为$x_i$的样本集合$m^{‘}$为阈值常数(默认30)。

$\hat{P}(c,x_i)=\frac{|D_{c,x_i}|+1}{|D|+N+N_i}$ $\hat{P}(x_j|c,x_i) = \frac{|D_{c,x_i,x_j}|+1}{|D_{c,x_i}|+N_j}$

其中N是D中可能的类别数，$N_i$是第i个属性可能的取值数，$D_{c,x_i}$是类别为c且在第i个属性上取值为$x_i$的样本集合，$D_{c, x_i, x_j}$是类别为c且在第i和第j个属性上分别为$x_i$和$x_j$的样本集合。