仿射变换&双线性插值

线性变换

在学习仿射变换之前，先看一下线性变换。
我们定义：

• 点$k$二维空间内一点，用列向量$\left[
  \begin{matrix}
  x \\y
  \end{matrix}
  \right]
  $表示
• 矩阵$M=\left[
  \begin{matrix}
  a & b \\c & d
  \end{matrix}
  \right]$表示一个$(2\times2)$的一个方阵

通过对$M$取不同的值，可以对$k$完成不同的线性变换。

$$K'=MK$$

例如，当$M=\left[
\begin{matrix}
1 & 0 \\0 & 1
\end{matrix}
\right]$时，

$$K'= \left[\begin{matrix}1 & 0 \\ 0 & 1 \end{matrix}\right] \left[\begin{matrix}x \\ y \end{matrix}\right]= \left[\begin{matrix}x \\ y \end{matrix}\right]=K$$

下面来看典型的基本线性变换是如何实现的。

放缩(Scaling)

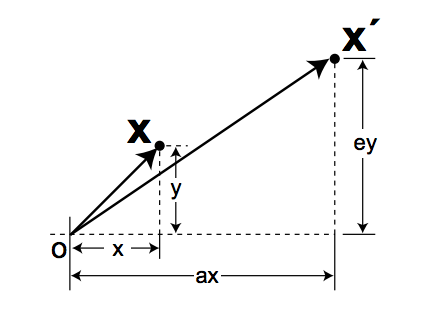
我们取$b=c=0$，$a$和$d$取任意整数：

$$M=\left[\begin{matrix}p & 0 \\ 0 & q \end{matrix}\right]$$

可以得到

$$K'= \left[\begin{matrix}p & 0 \\ 0 & q \end{matrix}\right] \left[\begin{matrix}x \\ y \end{matrix}\right]= \left[\begin{matrix}px \\ qy \end{matrix}\right]$$

旋转(Rotation)

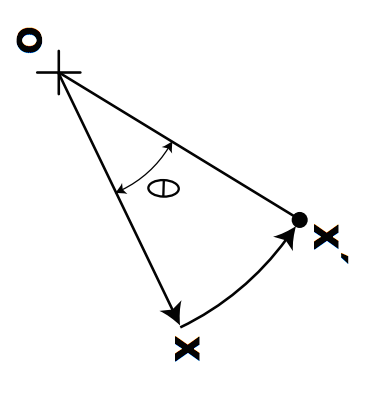
如图，假设我们想旋转$\theta$，那我们需要设置$a=d=\cos\theta,b=-\sin\theta,c=\sin\theta$

$$M=\left[\begin{matrix}\cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{matrix}\right]$$

旋转后的坐标

$$K'= \left[\begin{matrix}\cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{matrix}\right] \left[\begin{matrix}x \\ y \end{matrix}\right]= \left[\begin{matrix}x\cos\theta-y\sin\theta \\ x\sin\theta+y\cos\theta \end{matrix}\right]$$

旋转矩阵推导

裁剪(Shear)

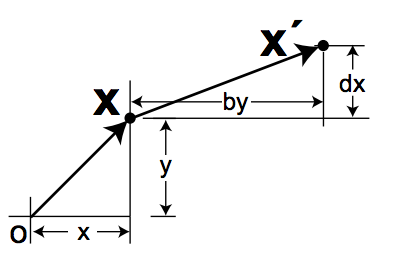
（好吧，这个变换我根本不懂什么意义）

小结

我们定义了3个基本的线性变换：

• 放缩：按标量缩放x和y方向。
• 旋转：将点绕原点旋转角度θ。
• 裁剪：将x偏移与y成正比的数字，并将x偏移与x成正比的数字。

由于矩阵乘法的交换律，我们可以把多个线性变换合成一个线性变换。
比如，我们要对$k$依次进行进行一次放缩变换$S$，一次裁剪变换$H$，一次旋转变换$R$。

$$K'=R[H(SK)]$$

由矩阵乘法的结合律得

$$K'=(RHS)K=MK$$

所以矩阵乘法有个好处：当我们进行多次线性变换的时候，不需要对进行多次矩阵乘法运算，只需要找到对的$M$，就可以一步到位！

仿射变换

简单来说，仿射变换就是：线性变换+平移

上面的变换可以将图像扭成任意形状，但在二维坐标系内，用2x2的矩阵所不能表示的变换就是平移操作。而平移是图像转换的重要变换.

所以，我们用一个三维的齐次坐标来表示二维向量：

• 点$k$用一个$(3\times1)$列向量$\left[\begin{matrix}x \\y \\1
  \end{matrix}\right]$表示
• 矩阵$M=\left[
  \begin{matrix}
  a & b & 0\\c & d & 0 \\0 & 0 & 1
  \end{matrix}
  \right]$表示一个$(3\times3)$的一个方阵

为了表示平移变换，我们只需要在$M$的第三列放两个新的参数$e,f$

$$M=\left[\begin{matrix} a & b & e\\ c & d & f \\0 & 0 & 1 \end{matrix}\right]$$

如果只需为二维输出，那么只要用一个$2\times3$的矩阵来表示$M$，就可以进行我们的仿射变换。

$$M=\left[\begin{matrix} a & b & e\\ c & d & f \end{matrix}\right]$$

双线性插值

当我们进行了仿射变换后，比如旋转或者放缩，得到左图各像素点在右图中对应的位置，但转换后的坐标往往不是整数。我们需要得到右图每个整数点的像素值才能渲染出这张image。所以要想点办法。

考虑到，我们将左图乘了一个$M$得到变换后的坐标，同样存在一种逆变换$M’$可以让我们将右图各像素点还原到左图相对应的位置。同样，这些位置虽然不一定是整数，但我们可以使用双线性插值等方法对其像素值进行估计。

所以在实际操作中所求的$M$其实是一种从后到前的逆变换。
（个人理解）

算法原理

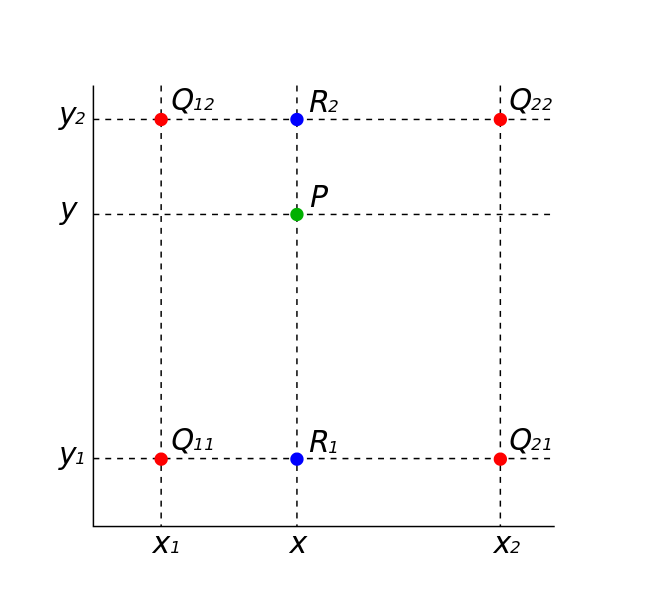
先做$x$轴方向的线性插值得到$R_2$和$R_1$。

$$R_1=\frac{x_2-x}{x_2-x_1}Q_{11}+\frac{x-x_1}{x_2-x_1}Q_{21}$$ $$R_2=\frac{x_2-x}{x_2-x_1}Q_{12}+\frac{x-x_1}{x_2-x_1}Q_{22}$$

再做$y$轴方向的线性插值

$$P=\frac{y_2-y}{y_2-y_1}R_1+\frac{y-y_1}{y_2-y_1}R_2$$

当然也可以先做$y$轴的插值在做$x$轴的插值。

代码

搬运：kevin’s blog