为什么要降维?
在原始的高维空间中,包含冗余信息和噪声信息,会在实际应用中引入误差,影响准确率;而降维可以提取数据内部的本质结构,减少冗余信息和噪声信息造成的误差,提高应用中的精度。
- 噪声
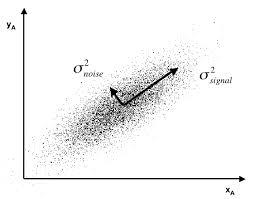
- 冗余
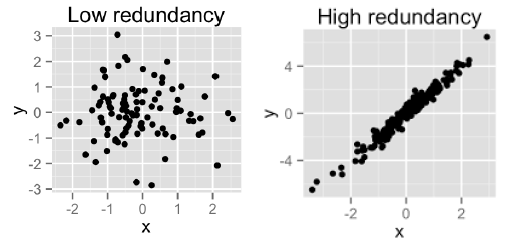
PCA思想
PCA顾名思义,就是找出数据里最主要的方面,用数据里最主要的方面来代替原始数据。
假设有$m$个数据样本$\boldsymbol{X}=\{\boldsymbol{x_1},\boldsymbol{x_2},…,\boldsymbol{x_m}\}$,每个样本是$n$维的$\boldsymbol{x_1}=(x_{i1},x_{i2},…,x_{in})$。我们希望将这$m$个数据的维度从$n$维降到$n’$维,希望这个$m$个$n’$维的数据集尽可能代表原数据集。我们知道数据从$n$维降到$n’$维肯定会有损失,但是我们希望损失尽可能的小。那么如何让这$n’$维的数据尽可能表示原来的数据呢?
现在我们的样本是再$n$维的空间里,希望投影到一个$n’$维的超平面。这样就实现了降维。如果存在这样的超平面,那么它大概具有这样的性质:
- 最近重构性:样本点到这个超平面的距离都足够近;
- 最大可分性:样本点在这个超平面上的投影尽可能分开。
基于最近重构性和最大可分性,分别得到主成分分析的两种等价推导。
基于最近重构性的PCA推导
假定样本进行了中心化,即$\sum_i\boldsymbol{x}_i=\boldsymbol{0}$;
假设投影变换后得到的新坐标系为$\{\boldsymbol{w}_1,\boldsymbol{w}_2,…,\boldsymbol{w}_d\}$,其中$\boldsymbol{w}_i$是标准正交基向量,即$\boldsymbol{w}_i^T\boldsymbol{w}_j=\delta_{ij}$;
那样本$\boldsymbol{x}_i$在另一个坐标系下的坐标为$(z_{i1}, z_{i2},…,z_{id})$,其中$z_{ij}=\boldsymbol{w}_j^T\boldsymbol{x}_i$是$\boldsymbol{x}_i$在低维坐标系下第$j$维的坐标。即$\boldsymbol{x}_i=\sum_{j=0}^dz_{ij}\boldsymbol{w}_j$。
若丢弃新坐标系中的部分坐标,将维度讲到$d’<d$,则$\boldsymbol{x}_i$的投影变为$\boldsymbol{z}_i = (z_{i1}, z_{i2},…,z_{id})$,再用$\boldsymbol{z}_i$来重构$\boldsymbol{x}_i$,则会有$\hat{\boldsymbol{x}}_i=\sum_{j=0}^{d’}z_{ij}\boldsymbol{w}_j$。
我们的目标是样本点到超平面的距离都足够近。也就是样本点$\boldsymbol{x}_i$到其在$d’$维子空间的超平面的投影点$\hat{\boldsymbol{x}}_i$的距离足够近:
在进行推导之前,先指明几个关系:
$\boldsymbol{W} = \{\boldsymbol{w}_1,\boldsymbol{w}_2,…,\boldsymbol{w}_d\}$,而我们取前$d’$个设为$\boldsymbol{W}_{d’} = \{\boldsymbol{w}_1,\boldsymbol{w}_2,…,\boldsymbol{w}_{d’}\}$。$\boldsymbol{W}_{d’}$中每个列向量是一个标准正交基,所以有$\boldsymbol{W}_{d’}^T\boldsymbol{W}_{d’}=\boldsymbol{I}$,但$\boldsymbol{W}_{d’}\boldsymbol{W}_{d’}^T\neq\boldsymbol{I}$.
规定了$\boldsymbol{W}_{d’}$,则$\boldsymbol{z}_i=\boldsymbol{W}_{d’}^T\boldsymbol{x}_i$,$\hat{\boldsymbol{x}}_i=\boldsymbol{W}_{d’}\boldsymbol{z}_i$.
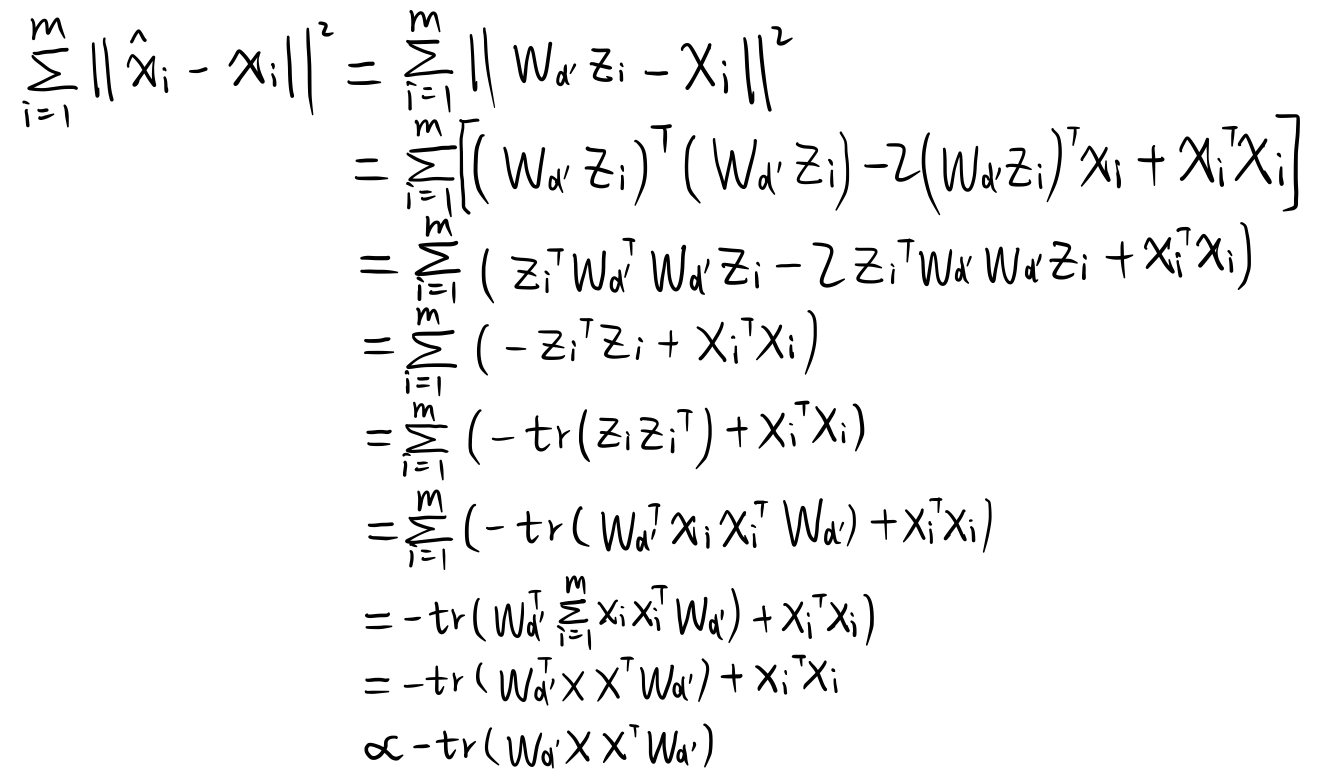
最小化上式等同于
这就是主成分分析的优化目标,可用拉格朗日乘子法求解。
拉格朗日函数
对$\boldsymbol{W}求导有$
即
于是,只需要对协方差矩阵$\boldsymbol{X}\boldsymbol{X}^T$进行特征值分解,将求得的特征值排序:$\lambda_1\geq\lambda_2\geq…\geq\lambda_{n’}$,取前$n’$个特征值对应的特征向量构成$\boldsymbol{W}^*=(\boldsymbol{w}_1,\boldsymbol{w}_2,…,\boldsymbol{w}_{n’})$.这就是主成分分析的解。
基于最近重构性的PCA推导
最大可分性是希望样本点的投影能尽可能分开,则应该是投影后的样本点方差最大化。
样本点$\boldsymbol{x}_i$在新空间中超平面上的投影为$\boldsymbol{W}^T\boldsymbol{x}_i$,投影后的样本方差为$\sum_i\boldsymbol{W}^T\boldsymbol{x}_i\boldsymbol{x}_i^T\boldsymbol{W}$,于是优化目标可写为